All Courses
Explore Courses UPSC Exam UPSC Test Series Free Notes EduRev Infinity Get the App Login Join for Free
Sign in Open App
CAT Exam  >  CAT Questions  >  There are 6 students A, B, C, D, E, F who app... Start Learning for Free
SaveJoin the Discussion on the App
There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students:
  1. The numerical sum of the ranks and the marks of C and D are the same.
  2. 88 was scored in Biology.
  3. 84 was scored in Computer Science and the one who scored it was the topper.
  4. The score in English was not 86.
  5. 82 was not scored in Maths.
  6. B was not second, the person who was second scored 82.
  7. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics.
  8. C had scored 86, but not in Physics.
  9. A did not score 84 or 89.
  10. D's score was in Maths.
Based on the information given above, answer the questions that follow.
 
Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?
    Correct answer is '6'. Can you explain this answer?
    FREE This question is part of
    Download PDF Attempt Test
    		Download PDF Attempt this Test
    Verified Answer
    There are 6 students A, B, C, D, E, F who appeared in 6 different subj...
    In these questions, we represent all possible alternatives in a tabular representation. With the help of the hints, we put a tick or a cross in each cell of the table if that particular cell is definitely true or if it is definitely false. After this, we again go over the table and eliminate any choice which has been rendered impossible by the hint. We represent the information in the question as follows:

    In the above representation, we have used the following abbreviations:
    In subjects: P - Physics
    C - Chemistry
    M - Maths
    B - Biology
    CS - Computer Science
    E - English
    We will start with the hints that give us direct information first.
    Using hint 7, neither A nor E had scored 82, nor were their scores scored in Biology or Physics.

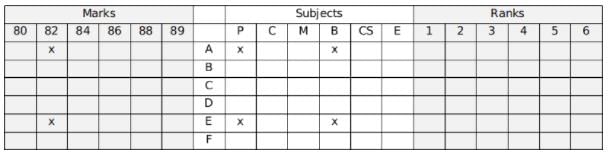
    Using hint 8, C had scored 86, but not in Physics.

    Using hint 10, D's score was in Maths.

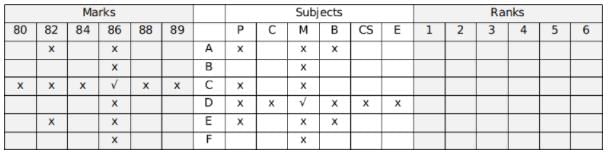
    Using hint 5, 82 was not scored in Maths.

    C scored 86 from point 8, also, 88 was scored in Biology and 84 was scored in Computer Science, so C did not appear in Biology or Computer Science.

    Using hint 4, the score in English was not 86.

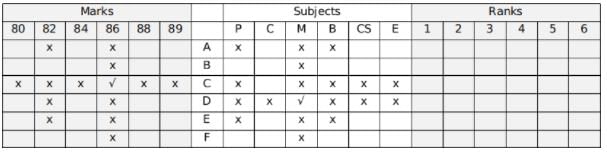
    Hence, C gave the Chemistry exam.

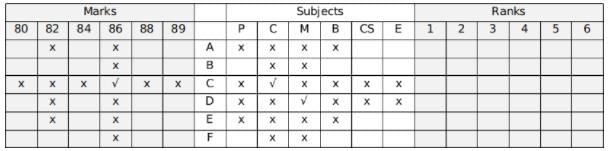
    Since B and F will score in Physics and Biology, A and E will score in Computer Science and English.

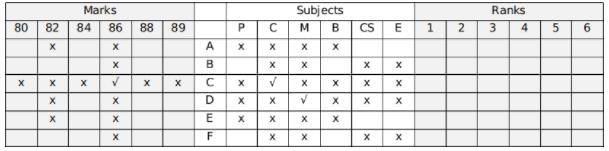
    Using hint 9, A did not score 84 or 89.

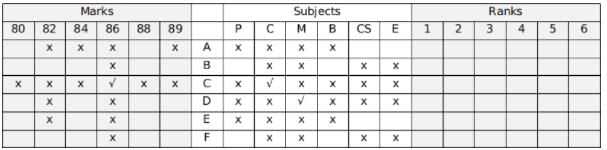
    Using hint 3, 84 was scored in Computer Science and the one who scored it was the topper.

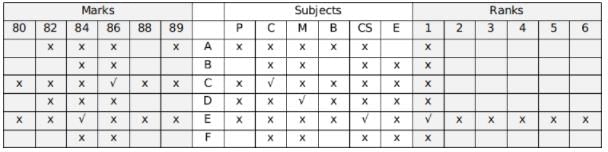
    Hence, A scored in English.

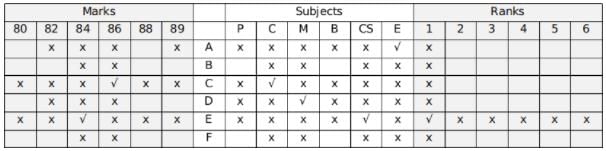
    Using hint 6, B was not second, the person who was second scored 82.

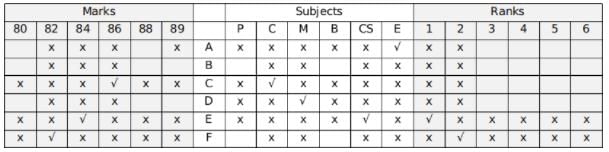
    Using hint 2, 88 was scored in Biology.

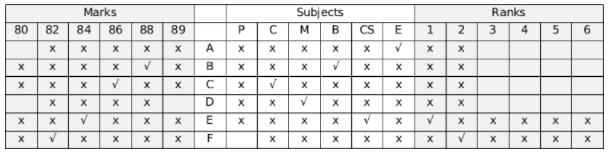
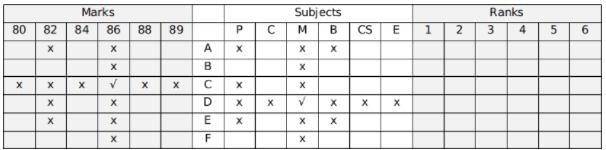
    Filling the remaining places,

    Using hint 1, the numerical sum of the ranks and the marks of C and D are the same.
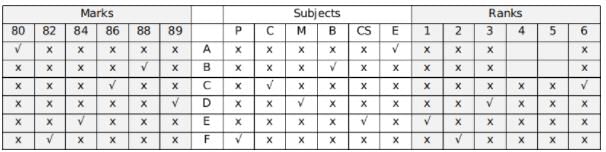
    Thus we can uniquely identify both the marks scored and the subject in which they appeared fro all 6 students.
    View all questions of this test
    Most Upvoted Answer
    There are 6 students A, B, C, D, E, F who appeared in 6 different subj...
    Analysis:

    • There are 6 students who appeared in 6 different subjects.

    • Each student got different marks from among 80, 82, 84, 86, 88, 89.

    • The ranks of the students in particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank.

    • The numerical sum of the ranks and the marks of C and D are the same.

    • 88 was scored in Biology.

    • 84 was scored in Computer Science and the one who scored it was the topper.

    • The score in English was not 86.

    • 82 was not scored in Maths.

    • B was not second, the person who was second scored 82.

    • Neither A nor E had scored 82, nor were their scores scored in Biology or Physics.

    • C had scored 86, but not in Physics.

    • A did not score 84 or 89.

    • D's score was in Maths.



    Solution:

    • The student who scored 88 is ranked 1 in Biology.

    • The student who scored 84 is ranked 1 in Computer Science.

    • The student who scored 86 is ranked 1 in a subject other than Physics.

    • D's score was in Maths, which means D is ranked 1 in Maths.

    • The person who scored 82 is ranked 2 in a subject other than Maths. So, B cannot be ranked 2.

    • Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. So, the remaining subjects for them are Chemistry, Computer Science, English, and Maths.

    • A did not score 84 or 89. So, A scored either 80, 82 or 86.

    • The score in English was not 86. So, E scored 86 in a subject other than English.

    • The numerical sum of the ranks and the marks of C and D are the same. So, either C scored 84 or D scored 88.

    • Since no two people got the same rank, C cannot be ranked 1 in Physics (as D is ranked 1 in Maths). So, C must be ranked 1 in Chemistry or English.

    • Thus, we can uniquely identify both the marks scored and the subject in which they appeared for all 6 students.



    Hence, the correct answer is '6'.
    Attention CAT Students!
    To make sure you are not studying endlessly, EduRev has designed CAT study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in CAT.
    < Previous Question Next Question >
    Explore Courses for CAT exam

    Similar CAT Doubts

    There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. In which subject was 80 scored?

    There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. Who scored 89?

    There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. Whose rank was 6?

    Direction: Study the following information carefully and answer the question given below:There are eight students i.e. A, B, C, D, E, F, G and H are studying in different classes i.e. V, VI, VII, VIII, IX, X, XI and XII of a school. They all like different subjects i.e. Biology, Physics, Mathematics, Chemistry, History, Geography, English and Hindi and different colours i.e. Red, Blue, White, Black, Green, Pink, Violet and Brown. All the information is not necessarily in the same order.E likes Physics and studies in the fourth-lowest class. The one who likes Pink is senior to the one who likes Violet. There is a difference of three classes between E and C who likes Black colour. A likes Red colour and Hindi. A is junior to B who likes Green colour. C is just a junior to G who likes Mathematics. B likes Chemistry but doesn’t like pink. F likes Blue colour but doesn’t study in VII class. Four students are junior to G but senior to D. There is a difference of two classes between D and H. The one who is just senior to H likes English. The one who likes History also likes Brown. The one who likes Biology doesn’t like the white colour. The one who studies in V class likes White colour.If the classes of the students who like English and Geography are interchanged by the teachers according to their class performance then who amongst the following is two class senior to H?

    Direction: Study the following information carefully and answer the question given below:There are eight students i.e. A, B, C, D, E, F, G and H are studying in different classes i.e. V, VI, VII, VIII, IX, X, XI and XII of a school. They all like different subjects i.e. Biology, Physics, Mathematics, Chemistry, History, Geography, English and Hindi and different colours i.e. Red, Blue, White, Black, Green, Pink, Violet and Brown. All the information is not necessarily in the same order.E likes Physics and studies in the fourth-lowest class. The one who likes Pink is senior to the one who likes Violet. There is a difference of three classes between E and C who likes Black colour. A likes Red colour and Hindi. A is junior to B who likes Green colour. C is just a junior to G who likes Mathematics. B likes Chemistry but doesn’t like pink colour. F likes Blue colour but doesn’t study in VII class. Four students are junior to G but senior to D. There is a difference of two classes between D and H. The one who is just senior to H likes English. The one who likes History also likes Brown. The one who likes Biology doesn’t like the white colour. The one who studies in V class likes White colour.How many students are junior to the one who likes Biology but senior to the one who likes Brown colour?

    Top Courses for CATView all

    Top Courses for CAT

    There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?Correct answer is '6'. Can you explain this answer?
    Question Description
    There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?Correct answer is '6'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?Correct answer is '6'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?Correct answer is '6'. Can you explain this answer?.
    Solutions for There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?Correct answer is '6'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
    Here you can find the meaning of There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?Correct answer is '6'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?Correct answer is '6'. Can you explain this answer?, a detailed solution for There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?Correct answer is '6'. Can you explain this answer? has been provided alongside types of There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?Correct answer is '6'. Can you explain this answer? theory, EduRev gives you an ample number of questions to practice There are 6 students A, B, C, D, E, F who appeared in 6 different subjects, Physics, Chemistry, Maths, Biology, Computer Science and English such that no two students appeared for the same subject. They got different marks from among 80, 82, 84, 86, 88, 89 and their ranks in the particular subjects are among 1, 2, 3, 4, 5, 6, such that no two people got the same rank. Also, the following information is known regarding these 6 students: The numerical sum of the ranks and the marks of C and D are the same. 88 was scored in Biology. 84 was scored in Computer Science and the one who scored it was the topper. The score in English was not 86. 82 was not scored in Maths. B was not second, the person who was second scored 82. Neither A nor E had scored 82, nor were their scores scored in Biology or Physics. C had scored 86, but not in Physics. A did not score 84 or 89. Ds score was in Maths.Based on the information given above, answer the questions that follow.Q. For how many people can we uniquely identify both the marks scored and the subject in which they appeared?Correct answer is '6'. Can you explain this answer? tests, examples and also practice CAT tests.
    Explore Courses for CAT exam

    Top Courses for CAT

    Explore Courses

    Suggested Free Tests

    Signup for Free!
    Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
    10M+ students study on EduRev
    Get App
    © EduRev
    Education Revolution
    Follow Us
    Signup to see your scores go up within 7 days!
    Access 1000+ FREE Docs, Videos and Tests
    Takes less than 10 seconds to signup