CAT Exam > CAT Questions > In an academy of 900 students, a poll was con...
Start Learning for Free
In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:
1. A total of 45 students do not follow any of the above-mentioned clubs.
2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.
3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.
4. Any student who follows Club D also necessarily follows Club C.
5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.
6. The number of students who are fans of C but not D is 407.
Based on the information given above, answer the questions that follow.
1. A total of 45 students do not follow any of the above-mentioned clubs.
2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.
3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.
4. Any student who follows Club D also necessarily follows Club C.
5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.
6. The number of students who are fans of C but not D is 407.
Based on the information given above, answer the questions that follow.
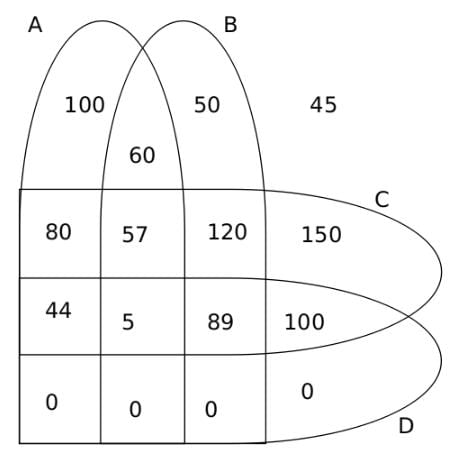
Q. How many students follow a maximum of 2 clubs?
Correct answer is '100'. Can you explain this answer?
Most Upvoted Answer
In an academy of 900 students, a poll was conducted as to which cricke...
This is a 4-circle Venn Diagram.
Also, point (4) mentions that anyone who follows D must necessarily follow C.
So, D is a subset of C.
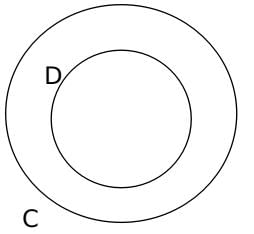
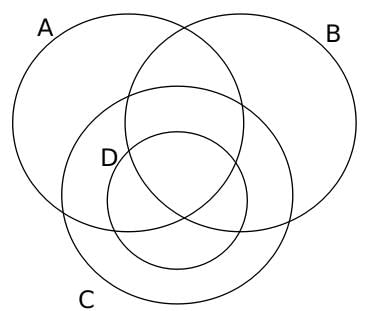
The entire Venn Diagram comes out as,
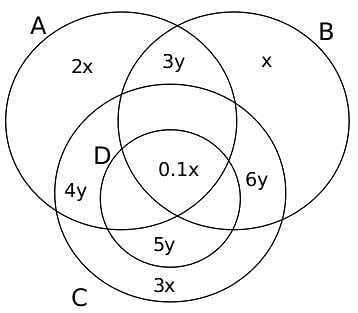
From point (2), let the number of students who follow only A be 2x, the number of students who follow only B be x and the number of students who follow only C be 3x.
Also, from point (3), the number of people who followed all of A, B, C and D = 2x/20 = x/10
Also from point (5), let the number of students who follow only A and B be 3y, the number of students who follow only A and C be 4y, the number of students who follow only C and D be 5y and the number of students who follow only B and C be 6y. Adding the same in the Venn Diagrams, we get:
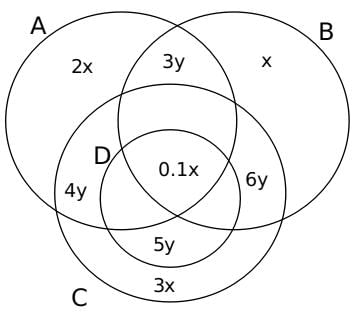
From point (5)
N2 + 8 + (N + 1)2 + 8 + (N + 3)2 + 8 = 190
N2 + (N + 1)2 + (N + 3)2 = 166
We can either expand the expression and solve the quadratic equation, or we can use hit and trial since we know that N is a natural number.
Solving, we get N = 6,
Hence, the number of students who follow only A, C and D = 44
The number of students who follow only A, B and C = 57
The number of students who follow only B, C and D = 89
Applying them in the Venn Diagram, we get,
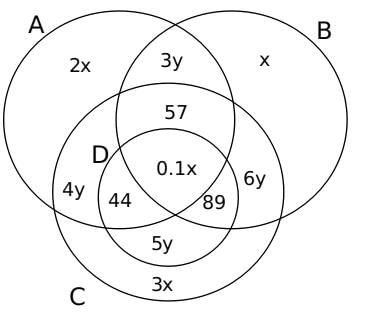
We know that the total number of students = 900, Hence,
2x + x + 3x + 0.1x + 3y + 4y + 5y + 6y + 44 + 57 + 89 + 45 = 900
6.1x + 18y = 665 ...(1)
Also, the number of students who are fans of C but not D = 407
Therefore, 4y + 3x + 6y + 57 = 407
3x + 10y = 350 ...(ii)
Solving equation 1 and 2 we get, x = 50 and y = 20
Hence the Venn Diagram comes out as,
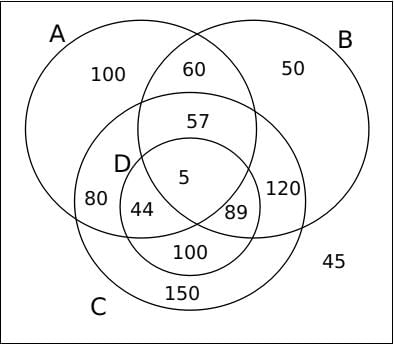
Number of students who follow a maximum of 2 clubs = Number of students who follow no club + Number of students who follow one club + Number of students who follow 2 clubs = 45 + 100 + 50 + 150 + 60 + 80 + 100 + 120 = 705
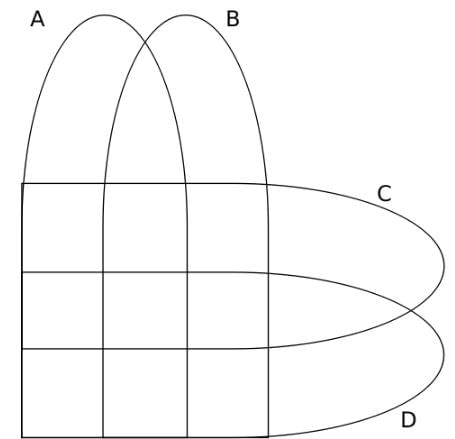
Alternate solution using 4-set Venn Diagram:
We can denote the 4-set Venn Diagram as follows:
Also, point (4) mentions that anyone who follows D must necessarily follow C.
From point (2), let the number of students who follow only A be 2x, the number of students who follow only B be x and the number of students who follow only C be 3x.
Also, from point (3), the number of people who followed all of A, B, C and D =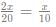
Also from point (5), let the number of students who follow only A and B be 3y, the number of students who follow only A and C be 4y, the number of students who follow only C and D be 5y and the number of students who follow only B and C be 6y. Adding the same in the Venn Diagrams, we get:

From point (5)
N2 + 8 + (N + 1)2 + 8 + (N + 3)2 + 8 = 190
N2 + (N + 1)2 + (N + 3)2 = 166
We can either expand the expression and solve the quadratic equation, or we can use hit and trial since we know that N is a natural number.
Solving, we get N = 6,
Hence, the number of students who follow only A, C and D = 44
The number of students who follow only A, B and C = 57
The number of students who follow only B, C and D = 89
Applying them in the Venn Diagram, we get,

We know that the total number of students = 900, Hence,
2x + x + 3x + 0.1x + 3y+ 4y + 5y + 6y + 44 + 57 + 89 + 45 = 900
6.1x + 18y = 665 .......(i)
Also, the number of students who are fans of C but not D = 407
Therefore, 4y + 3x + 6y + 57 = 407
3x + 10y = 350 .......(ii)
Solving equation 1 and 2 we get, x = 50 and y = 20
Hence the Venn Diagram comes out as,
The number of students who follow only C and D is 100.
Also, point (4) mentions that anyone who follows D must necessarily follow C.
So, D is a subset of C.

The entire Venn Diagram comes out as,

From point (2), let the number of students who follow only A be 2x, the number of students who follow only B be x and the number of students who follow only C be 3x.
Also, from point (3), the number of people who followed all of A, B, C and D = 2x/20 = x/10
Also from point (5), let the number of students who follow only A and B be 3y, the number of students who follow only A and C be 4y, the number of students who follow only C and D be 5y and the number of students who follow only B and C be 6y. Adding the same in the Venn Diagrams, we get:

From point (5)
N2 + 8 + (N + 1)2 + 8 + (N + 3)2 + 8 = 190
N2 + (N + 1)2 + (N + 3)2 = 166
We can either expand the expression and solve the quadratic equation, or we can use hit and trial since we know that N is a natural number.
Solving, we get N = 6,
Hence, the number of students who follow only A, C and D = 44
The number of students who follow only A, B and C = 57
The number of students who follow only B, C and D = 89
Applying them in the Venn Diagram, we get,

We know that the total number of students = 900, Hence,
2x + x + 3x + 0.1x + 3y + 4y + 5y + 6y + 44 + 57 + 89 + 45 = 900
6.1x + 18y = 665 ...(1)
Also, the number of students who are fans of C but not D = 407
Therefore, 4y + 3x + 6y + 57 = 407
3x + 10y = 350 ...(ii)
Solving equation 1 and 2 we get, x = 50 and y = 20
Hence the Venn Diagram comes out as,

Number of students who follow a maximum of 2 clubs = Number of students who follow no club + Number of students who follow one club + Number of students who follow 2 clubs = 45 + 100 + 50 + 150 + 60 + 80 + 100 + 120 = 705
Alternate solution using 4-set Venn Diagram:
We can denote the 4-set Venn Diagram as follows:

Also, point (4) mentions that anyone who follows D must necessarily follow C.

From point (2), let the number of students who follow only A be 2x, the number of students who follow only B be x and the number of students who follow only C be 3x.
Also, from point (3), the number of people who followed all of A, B, C and D =
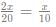
Also from point (5), let the number of students who follow only A and B be 3y, the number of students who follow only A and C be 4y, the number of students who follow only C and D be 5y and the number of students who follow only B and C be 6y. Adding the same in the Venn Diagrams, we get:

From point (5)
N2 + 8 + (N + 1)2 + 8 + (N + 3)2 + 8 = 190
N2 + (N + 1)2 + (N + 3)2 = 166
We can either expand the expression and solve the quadratic equation, or we can use hit and trial since we know that N is a natural number.
Solving, we get N = 6,
Hence, the number of students who follow only A, C and D = 44
The number of students who follow only A, B and C = 57
The number of students who follow only B, C and D = 89
Applying them in the Venn Diagram, we get,

We know that the total number of students = 900, Hence,
2x + x + 3x + 0.1x + 3y+ 4y + 5y + 6y + 44 + 57 + 89 + 45 = 900
6.1x + 18y = 665 .......(i)
Also, the number of students who are fans of C but not D = 407
Therefore, 4y + 3x + 6y + 57 = 407
3x + 10y = 350 .......(ii)
Solving equation 1 and 2 we get, x = 50 and y = 20
Hence the Venn Diagram comes out as,

The number of students who follow only C and D is 100.
Community Answer
In an academy of 900 students, a poll was conducted as to which cricke...
This is a 4-circle Venn Diagram.
Also, point (4) mentions that anyone who follows D must necessarily follow C.
So, D is a subset of C.
The entire Venn Diagram comes out as,

From point (2), let the number of students who follow only A be 2x, the number of students who follow only B be x and the number of students who follow only C be 3x.
Also, from point (3), the number of people who followed all of A, B, C and D = 2x/20 = x/10
Also from point (5), let the number of students who follow only A and B be 3y, the number of students who follow only A and C be 4y, the number of students who follow only C and D be 5y and the number of students who follow only B and C be 6y. Adding the same in the Venn Diagrams, we get:
From point (5)
N2 + 8 + (N + 1)2 + 8 + (N + 3)2 + 8 = 190
N2 + (N + 1)2 + (N + 3)2 = 166
We can either expand the expression and solve the quadratic equation, or we can use hit and trial since we know that N is a natural number.
Solving, we get N = 6,
Hence, the number of students who follow only A, C and D = 44
The number of students who follow only A, B and C = 57
The number of students who follow only B, C and D = 89
Applying them in the Venn Diagram, we get,
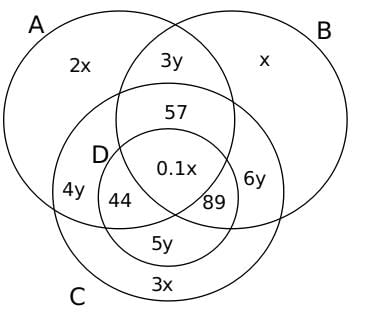
We know that the total number of students = 900, Hence,
2x + x + 3x + 0.1x + 3y + 4y + 5y + 6y + 44 + 57 + 89 + 45 = 900
6.1x + 18y = 665 ...(1)
Also, the number of students who are fans of C but not D = 407
Therefore, 4y + 3x + 6y + 57 = 407
3x + 10y = 350 ...(ii)
Solving equation 1 and 2 we get, x = 50 and y = 20
Hence the Venn Diagram comes out as,
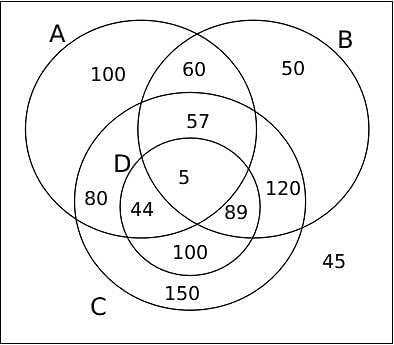
Number of students who follow a maximum of 2 clubs = Number of students who follow no club + Number of students who follow one club + Number of students who follow 2 clubs = 45 + 100 + 50 + 150 + 60 + 80 + 100 + 120 = 705
Alternate solution using 4-set Venn Diagram:
We can denote the 4-set Venn Diagram as follows:
Also, point (4) mentions that anyone who follows D must necessarily follow C.
From point (2), let the number of students who follow only A be 2x, the number of students who follow only B be x and the number of students who follow only C be 3x.
Also, from point (3), the number of people who followed all of A, B, C and D =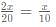
Also from point (5), let the number of students who follow only A and B be 3y, the number of students who follow only A and C be 4y, the number of students who follow only C and D be 5y and the number of students who follow only B and C be 6y. Adding the same in the Venn Diagrams, we get:

From point (5)
N2 + 8 + (N + 1)2 + 8 + (N + 3)2 + 8 = 190
N2 + (N + 1)2 + (N + 3)2 = 166
We can either expand the expression and solve the quadratic equation, or we can use hit and trial since we know that N is a natural number.
Solving, we get N = 6,
Hence, the number of students who follow only A, C and D = 44
The number of students who follow only A, B and C = 57
The number of students who follow only B, C and D = 89
Applying them in the Venn Diagram, we get,
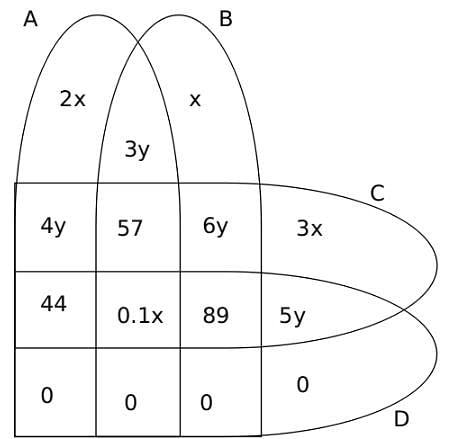
We know that the total number of students = 900, Hence,
2x + x + 3x + 0.1x + 3y+ 4y + 5y + 6y + 44 + 57 + 89 + 45 = 900
6.1x + 18y = 665 .......(i)
Also, the number of students who are fans of C but not D = 407
Therefore, 4y + 3x + 6y + 57 = 407
3x + 10y = 350 .......(ii)
Solving equation 1 and 2 we get, x = 50 and y = 20
Hence the Venn Diagram comes out as,
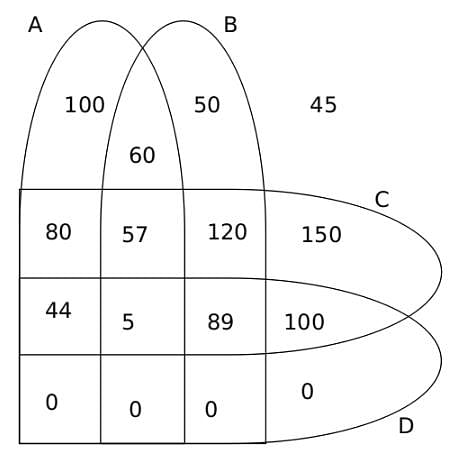
The number of students who follow only C and D is 100.
Also, point (4) mentions that anyone who follows D must necessarily follow C.
So, D is a subset of C.

The entire Venn Diagram comes out as,

From point (2), let the number of students who follow only A be 2x, the number of students who follow only B be x and the number of students who follow only C be 3x.
Also, from point (3), the number of people who followed all of A, B, C and D = 2x/20 = x/10
Also from point (5), let the number of students who follow only A and B be 3y, the number of students who follow only A and C be 4y, the number of students who follow only C and D be 5y and the number of students who follow only B and C be 6y. Adding the same in the Venn Diagrams, we get:

From point (5)
N2 + 8 + (N + 1)2 + 8 + (N + 3)2 + 8 = 190
N2 + (N + 1)2 + (N + 3)2 = 166
We can either expand the expression and solve the quadratic equation, or we can use hit and trial since we know that N is a natural number.
Solving, we get N = 6,
Hence, the number of students who follow only A, C and D = 44
The number of students who follow only A, B and C = 57
The number of students who follow only B, C and D = 89
Applying them in the Venn Diagram, we get,

We know that the total number of students = 900, Hence,
2x + x + 3x + 0.1x + 3y + 4y + 5y + 6y + 44 + 57 + 89 + 45 = 900
6.1x + 18y = 665 ...(1)
Also, the number of students who are fans of C but not D = 407
Therefore, 4y + 3x + 6y + 57 = 407
3x + 10y = 350 ...(ii)
Solving equation 1 and 2 we get, x = 50 and y = 20
Hence the Venn Diagram comes out as,

Number of students who follow a maximum of 2 clubs = Number of students who follow no club + Number of students who follow one club + Number of students who follow 2 clubs = 45 + 100 + 50 + 150 + 60 + 80 + 100 + 120 = 705
Alternate solution using 4-set Venn Diagram:
We can denote the 4-set Venn Diagram as follows:

Also, point (4) mentions that anyone who follows D must necessarily follow C.

From point (2), let the number of students who follow only A be 2x, the number of students who follow only B be x and the number of students who follow only C be 3x.
Also, from point (3), the number of people who followed all of A, B, C and D =
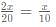
Also from point (5), let the number of students who follow only A and B be 3y, the number of students who follow only A and C be 4y, the number of students who follow only C and D be 5y and the number of students who follow only B and C be 6y. Adding the same in the Venn Diagrams, we get:

From point (5)
N2 + 8 + (N + 1)2 + 8 + (N + 3)2 + 8 = 190
N2 + (N + 1)2 + (N + 3)2 = 166
We can either expand the expression and solve the quadratic equation, or we can use hit and trial since we know that N is a natural number.
Solving, we get N = 6,
Hence, the number of students who follow only A, C and D = 44
The number of students who follow only A, B and C = 57
The number of students who follow only B, C and D = 89
Applying them in the Venn Diagram, we get,

We know that the total number of students = 900, Hence,
2x + x + 3x + 0.1x + 3y+ 4y + 5y + 6y + 44 + 57 + 89 + 45 = 900
6.1x + 18y = 665 .......(i)
Also, the number of students who are fans of C but not D = 407
Therefore, 4y + 3x + 6y + 57 = 407
3x + 10y = 350 .......(ii)
Solving equation 1 and 2 we get, x = 50 and y = 20
Hence the Venn Diagram comes out as,

The number of students who follow only C and D is 100.

|
Explore Courses for CAT exam
|

|
Similar CAT Doubts
In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer?
Question Description
In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer?.
In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer? for CAT 2025 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer? covers all topics & solutions for CAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer?.
Solutions for In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT.
Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.
Here you can find the meaning of In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer?, a detailed solution for In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer? has been provided alongside types of In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In an academy of 900 students, a poll was conducted as to which cricket clubs the students follow regularly. There was a list of 4 top clubs A, B, C and D. The following points are known regarding the results of the poll:1. A total of 45 students do not follow any of the above-mentioned clubs.2. Ratio of the students who follow only A to those who follow only B to those who follow only C is 2:1:3.3. The number of students who follow only A is 20 times the number of students who follow all the 4 clubs.4. Any student who follows Club D also necessarily follows Club C.5. Ratio of the students who follow only A and B to those who follow only A and C to those who follow only C and D to those who follow only B and C is 3:4:5:6. Also, it is known that the number of students who follow only A, C and D, the number of students who follow only A, B and C, and the number of students who follow only B, C and D are in the form of N2 + 8, (N + 1)2 + 8 and (N + 3)2 + 8 respectively, where N is a natural number and the sum of the number of these students is 190.6. The number of students who are fans of C but not D is 407.Based on the information given above, answer the questions that follow.Q.How many students follow a maximum of 2 clubs?Correct answer is '100'. Can you explain this answer? tests, examples and also practice CAT tests.

|
Explore Courses for CAT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























