Class 12 Exam > Class 12 Questions > A thin prism with an angle of 3o and made fro...
Start Learning for Free
A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?
- a)3o
- b)0o
- c)1o
- d)2o
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
A thin prism with an angle of 3o and made from glass of refractive ind...
In order to understand why the correct answer is option 'C', let's break down the problem into different parts and analyze each step.
1. Understanding the problem:
We have two prisms made from different types of glass, each with their own refractive index. The first prism has an angle of 30 degrees and a refractive index of 1.15. We need to find the angle of the second prism when dispersion occurs without deviation.
2. Dispersion without deviation:
Dispersion refers to the phenomenon where different colors of light separate when passing through a medium. Deviation occurs when light changes direction upon entering a different medium, due to refraction. However, in this case, we are specifically looking for dispersion without deviation. This means that the light should separate into different colors without changing its overall direction.
3. Snell's Law:
Snell's Law is the principle that describes the relationship between the angles of incidence and refraction when light passes through a boundary between two media. It is given by the equation:
n1 * sin(θ1) = n2 * sin(θ2)
Where n1 and n2 are the refractive indices of the first and second media, θ1 is the angle of incidence, and θ2 is the angle of refraction.
4. Applying Snell's Law to the problem:
Since the first prism is made of glass with a refractive index of 1.15, and the second prism is made of glass with a refractive index of 1.45, we can apply Snell's Law to find the angle of refraction for each prism.
For the first prism:
n1 * sin(θ1) = n2 * sin(θ2)
1.00 * sin(30°) = 1.15 * sin(θ2)
sin(θ2) = (1.00 * sin(30°)) / 1.15
θ2 ≈ 16.67°
For the second prism:
n1 * sin(θ1) = n2 * sin(θ2)
1.15 * sin(θ2) = 1.45 * sin(θ3)
θ3 ≈ 36.12°
5. Conclusion:
From the calculations, we find that the angle of the second prism, when dispersion occurs without deviation, is approximately 36.12°. Therefore, the correct answer is option 'C'.
1. Understanding the problem:
We have two prisms made from different types of glass, each with their own refractive index. The first prism has an angle of 30 degrees and a refractive index of 1.15. We need to find the angle of the second prism when dispersion occurs without deviation.
2. Dispersion without deviation:
Dispersion refers to the phenomenon where different colors of light separate when passing through a medium. Deviation occurs when light changes direction upon entering a different medium, due to refraction. However, in this case, we are specifically looking for dispersion without deviation. This means that the light should separate into different colors without changing its overall direction.
3. Snell's Law:
Snell's Law is the principle that describes the relationship between the angles of incidence and refraction when light passes through a boundary between two media. It is given by the equation:
n1 * sin(θ1) = n2 * sin(θ2)
Where n1 and n2 are the refractive indices of the first and second media, θ1 is the angle of incidence, and θ2 is the angle of refraction.
4. Applying Snell's Law to the problem:
Since the first prism is made of glass with a refractive index of 1.15, and the second prism is made of glass with a refractive index of 1.45, we can apply Snell's Law to find the angle of refraction for each prism.
For the first prism:
n1 * sin(θ1) = n2 * sin(θ2)
1.00 * sin(30°) = 1.15 * sin(θ2)
sin(θ2) = (1.00 * sin(30°)) / 1.15
θ2 ≈ 16.67°
For the second prism:
n1 * sin(θ1) = n2 * sin(θ2)
1.15 * sin(θ2) = 1.45 * sin(θ3)
θ3 ≈ 36.12°
5. Conclusion:
From the calculations, we find that the angle of the second prism, when dispersion occurs without deviation, is approximately 36.12°. Therefore, the correct answer is option 'C'.
Free Test
FREE
| Start Free Test |
Community Answer
A thin prism with an angle of 3o and made from glass of refractive ind...
The required equation
⇒ δ = (μ - 1)A
When two prisms are combined, then:
δ = δ + δ’ = (μ - 1)A + (μ’ - 1)A’ = 0
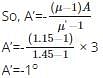
Therefore, the angle of the other prism is 1o and opposite of the first prism.
⇒ δ = (μ - 1)A
When two prisms are combined, then:
δ = δ + δ’ = (μ - 1)A + (μ’ - 1)A’ = 0
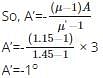
Therefore, the angle of the other prism is 1o and opposite of the first prism.

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer?
Question Description
A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer?.
A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer? for Class 12 2024 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Class 12 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A thin prism with an angle of 3o and made from glass of refractive index 1.15 is combined with another prism made from glass and has a refractive index of 1.45. If the dispersion were to occur without deviation then what should be the angle of the second prism?a)3ob)0oc)1od)2oCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















