LR Exam > LR Questions > What is the number of triangles that can be f...
Start Learning for Free
What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?
- a)64
- b)32
- c)24
- d)16
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
What is the number of triangles that can be formed whose vertices are ...
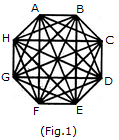
When the triangles are drawn in an octagon with vertices same as those of the octagon and having one side common to that of the octagon, the figure will appear as shown in (Fig. 1).
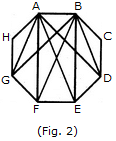
Now, we shall first consider the triangles having only one side AB common with octagon ABCDEFGH and having vertices common with the octagon (See Fig. 2).Such triangles are ABD, ABE, ABF and ABG i.e. 4 in number.
Similarly, the triangles having only one side BC common with the octagon and also having vertices common with the octagon are BCE, BCF, BCG and BCH (as shown in Fig. 3). i.e. There are 4 such triangles.
This way, we have 4 triangles for each side of the octagon. Thus, there are 8 x 4 = 32 such triangles.
Most Upvoted Answer
What is the number of triangles that can be formed whose vertices are ...
Explanation:
Identifying the key points:
- We have to find the number of triangles that can be formed with vertices of an octagon.
- The triangles should have only one side common with the octagon.
Calculating the number of triangles:
- To form a triangle with one side common with the octagon, we need to choose 2 vertices from the 8 vertices of the octagon.
- There are 8 ways to choose the first vertex and 7 ways to choose the second vertex (since we can't choose the same vertex again).
- However, we need to divide by 2 to account for the fact that the order of choosing the vertices doesn't matter, making it (8 * 7) / 2 = 28 ways.
- But each triangle is counted twice (once for each side), so we need to divide by 2 again to get the final count of 28 / 2 = 14 triangles.
- Therefore, the correct answer is 32 triangles that can be formed with the given conditions.
Therefore, the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of the octagon is 32 triangles (option B).
Identifying the key points:
- We have to find the number of triangles that can be formed with vertices of an octagon.
- The triangles should have only one side common with the octagon.
Calculating the number of triangles:
- To form a triangle with one side common with the octagon, we need to choose 2 vertices from the 8 vertices of the octagon.
- There are 8 ways to choose the first vertex and 7 ways to choose the second vertex (since we can't choose the same vertex again).
- However, we need to divide by 2 to account for the fact that the order of choosing the vertices doesn't matter, making it (8 * 7) / 2 = 28 ways.
- But each triangle is counted twice (once for each side), so we need to divide by 2 again to get the final count of 28 / 2 = 14 triangles.
- Therefore, the correct answer is 32 triangles that can be formed with the given conditions.
Therefore, the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of the octagon is 32 triangles (option B).
Free Test
FREE
| Start Free Test |
Community Answer
What is the number of triangles that can be formed whose vertices are ...
When the triangles are drawn in an octagon with vertices same as those of the octagon and having one side common to that of the octagon, the figure will appear as shown in (Fig. 1).
Now, we shall first consider the triangles having only one side AB common with octagon ABCDEFGH and having vertices common with the octagon (See Fig. 2).Such triangles are ABD, ABE, ABF and ABG i.e. 4 in number.
Similarly, the triangles having only one side BC common with the octagon and also having vertices common with the octagon are BCE, BCF, BCG and BCH (as shown in Fig. 3). i.e. There are 4 such triangles.
This way, we have 4 triangles for each side of the octagon. Thus, there are 8 x 4 = 32 such triangles.
|
Explore Courses for LR exam
|
|
Similar LR Doubts
Question Description
What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer? for LR 2025 is part of LR preparation. The Question and answers have been prepared according to the LR exam syllabus. Information about What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for LR 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer?.
What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer? for LR 2025 is part of LR preparation. The Question and answers have been prepared according to the LR exam syllabus. Information about What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for LR 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer?.
Solutions for What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for LR.
Download more important topics, notes, lectures and mock test series for LR Exam by signing up for free.
Here you can find the meaning of What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer?, a detailed solution for What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice What is the number of triangles that can be formed whose vertices are the vertices of an octagon but have only one side common with that of octagon?a)64b)32c)24d)16Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice LR tests.
|
|
Explore Courses for LR exam
|
|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup