What is difference between escape velocity and orbital velocity

Question

Answer

Escape velocity

“The velocity required by a body to escape from the earth’s gravitational field.”It is our daily life experience that an object projected upward comes back to the ground after rising to a certain height. This is due to the force of gravity acting downward. With increased initial velocity, the object rises to the greater height before coming back. If we go on increasing the initial velocity of the object,a stage comes when it will not return to the ground. It will escape out of the influence of gravity. The initial velocity of an object with which it goes out of the earth’s gravitational field is known as E.V.

Escape velocity formula

The E.V corresponds to the initial kinetic energy gained by the body,which carries it to an infinite distance from the surface of earth.

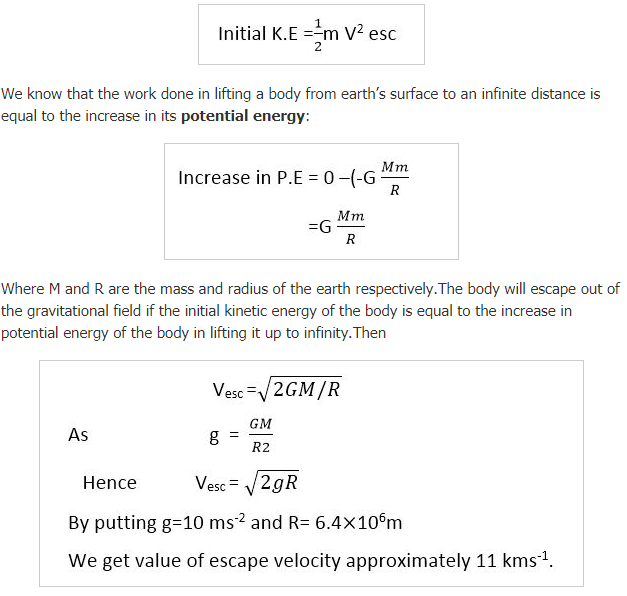
Orbital velocity

When the object in the earths orbit ,its motion is known as orbital motion.The velocity by which the object moves in the earth’s orbit is called orbital velocity.It remains constant in the gravitational field.

The earth and some other planets revolve around the sun in closely circular paths.The artificial satellites launched by men also adopt nearly circular course around the earth.This type of motion is called orbital motion.Formula of this velocity is given as:

Consider a satellite going round the earth in circular path.The mass of the satellite is m and v� is the orbital speed.The mass of the Earth is M and r� represents the radius of orbit.A centripetal force is required to hold satellite in orbit which is given as:

Answer

The orbital velocity is the velocity an object must maintain in order to be on a certain orbit. For an object going on an orbit with radius r, the orbital velocity is given by the square root of (F r / m) where F is the net inward force and m is the mass of the orbital object. The inward force in a mass system is GMm/r2. By substituting this, we get the orbital velocity as the square root of (GM/r). This also can be proved using mechanical energy conservation of a conservative field.As we know from the gravitational field theory, an object having a mass always attracts any other object which is placed in a finite distance from the object. As the distance increases the force between the two objects lowers with the inverse square of the distance. At infinity, the force between the two objects is zero. The potential of a point around a mass is defined as the work that has to be done to bring an object of unit mass from infinity to the given point.

The orbital velocity is the velocity an object must maintain in order to be on a certain orbit. For an object going on an orbit with radius r, the orbital velocity is given by the square root of (F r / m) where F is the net inward force and m is the mass of the orbital object. The inward force in a mass system is GMm/r2. By substituting this, we get the orbital velocity as the square root of (GM/r). This also can be proved using mechanical energy conservation of a conservative field.

As we know from the gravitational field theory, an object having a mass always attracts any other object which is placed in a finite distance from the object. As the distance increases the force between the two objects lowers with the inverse square of the distance. At infinity, the force between the two objects is zero. The potential of a point around a mass is defined as the work that has to be done to bring an object of unit mass from infinity to the given point.

Answer

Escape Velocity:
Escape velocity is the minimum velocity required for an object to escape the gravitational pull of a planet, moon, or any celestial body. It is the speed at which an object needs to travel in order to overcome the gravitational force and move away indefinitely from the body's influence. Here are the key points to understand about escape velocity:

1. Definition: Escape velocity can be defined as the speed required for an object to escape the gravitational field of a planet or any other celestial body without any further propulsion.

2. Calculation: Escape velocity can be calculated using the formula: v = √(2GM/r), where v is the escape velocity, G is the gravitational constant, M is the mass of the celestial body, and r is the distance from the center of the celestial body.

3. Independence of Mass: The escape velocity does not depend on the mass of the object being launched. It only depends on the mass and radius of the celestial body.

4. Leaving the Gravitational Field: If an object is launched with a velocity less than the escape velocity, it will follow a curved trajectory and eventually fall back to the surface. On the other hand, if the object is launched with a velocity greater than or equal to the escape velocity, it will leave the gravitational field.

5. Examples: For example, the escape velocity on Earth is approximately 11.2 km/s, while the escape velocity on the Moon is about 2.4 km/s.

Orbital Velocity:
Orbital velocity is the minimum velocity required for an object to maintain a stable orbit around a celestial body. It is the speed at which an object needs to travel to balance the gravitational force and centrifugal force acting on it. Here are the key points to understand about orbital velocity:

1. Definition: Orbital velocity can be defined as the speed required for an object to maintain a stable orbit around a celestial body without any further propulsion.

2. Calculation: Orbital velocity can be calculated using the formula: v = √(GM/r), where v is the orbital velocity, G is the gravitational constant, M is the mass of the celestial body, and r is the distance from the center of the celestial body.

3. Dependence on Distance: The orbital velocity depends on the distance from the center of the celestial body. As the distance increases, the orbital velocity decreases.

4. Circular Orbits: In a circular orbit, the orbital velocity remains constant throughout the orbit. The gravitational force and centrifugal force acting on the object balance each other, resulting in a stable circular path.

5. Elliptical Orbits: In an elliptical orbit, the orbital velocity varies at different points along the orbit. The object moves faster when it is closer to the celestial body and slower when it is farther away.

6. Examples: The orbital velocity of the International Space Station (ISS) is approximately 28,000 km/h, while the orbital velocity of the Moon around the Earth is about 1 km/s.

In conclusion, escape velocity is the speed required to escape the gravitational pull of a celestial body, while orbital velocity is the speed required to maintain a stable orbit around a celestial body. The escape velocity allows an object to leave the gravitational field, whereas the orbital velocity allows an object to stay in orbit without falling back to the surface.

Similar Class 11 Doubts

What is the difference between atomic orbital and molecular orbital?

Difference between orbit and orbital

Needed a Document for gravitational notes in hindi? Related: Orbital and Escape Velocity (Part - 1)?

what is escape Velocity derivatives Related: Orbital and Escape Velocity (Part - 1)?

Find the expression for orbital speed & escape velocity for Sattelite ?

Top Courses for Class 11View all

Chemistry Class 11

CUET Mock Test: Humanities Subjects 2025

English Class 11

Mathematics (Maths) Class 11

Psychology CUET UG Mock Test Series 2025

Top Courses for Class 11

Top Courses for Class 11

Related Content

Schools

Competitive Examinations

Quick Access Links

Technical Exams