Class 9 Exam > Class 9 Questions > If the radius and height of a cone both are i...
Start Learning for Free
If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ?
Verified Answer
If the radius and height of a cone both are increased by 10% then the ...
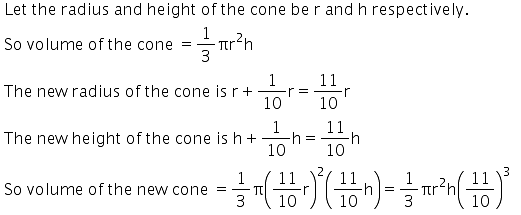
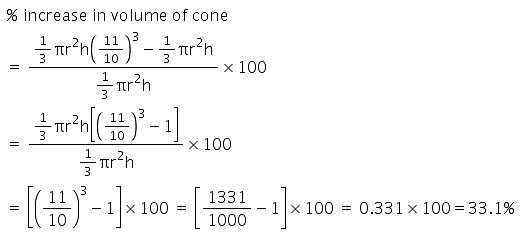
 This question is part of UPSC exam. View all Class 9 courses
This question is part of UPSC exam. View all Class 9 courses
Most Upvoted Answer
If the radius and height of a cone both are increased by 10% then the ...
Increasing the Radius and Height of a Cone
To find out how much the volume of a cone increases when both the radius and height are increased by 10%, we can follow these steps:
1. Determine the formula for the volume of a cone:
The volume of a cone can be calculated using the formula V = (1/3)πr²h, where V represents the volume, π is a mathematical constant (approximately 3.14159), r is the radius, and h is the height of the cone.
2. Calculate the initial volume of the cone:
Let's assume the initial radius of the cone is r and the initial height is h. Using the volume formula, we can calculate the initial volume as V1 = (1/3)πr²h.
3. Calculate the increased radius and height:
Since both the radius and height are increased by 10%, we can calculate the new values as follows:
- Increased radius: r + 10% of r = r + 0.1r = 1.1r
- Increased height: h + 10% of h = h + 0.1h = 1.1h
4. Calculate the increased volume of the cone:
After obtaining the increased radius (1.1r) and height (1.1h), we can calculate the new volume using the volume formula:
V2 = (1/3)π(1.1r)²(1.1h)
5. Calculate the percentage increase in volume:
To find the percentage increase in volume, we need to compare the initial volume (V1) with the increased volume (V2). The percentage increase can be calculated using the formula:
Percentage Increase = ((V2 - V1) / V1) * 100
Example:
Let's consider an example to illustrate the calculation. Suppose the initial radius (r) of a cone is 5 units and the initial height (h) is 8 units.
1. Calculate the initial volume:
V1 = (1/3)π(5)²(8) = (1/3)π(25)(8) ≈ 209.44 cubic units
2. Calculate the increased radius and height:
Increased radius = 5 + 0.1(5) = 5 + 0.5 = 5.5 units
Increased height = 8 + 0.1(8) = 8 + 0.8 = 8.8 units
3. Calculate the increased volume:
V2 = (1/3)π(5.5)²(8.8) ≈ 266.71 cubic units
4. Calculate the percentage increase in volume:
Percentage Increase = ((266.71 - 209.44) / 209.44) * 100 ≈ 27.37%
Conclusion:
When both the radius and height of a cone are increased by 10%, the volume of the cone increases by approximately 27.37%.
To find out how much the volume of a cone increases when both the radius and height are increased by 10%, we can follow these steps:
1. Determine the formula for the volume of a cone:
The volume of a cone can be calculated using the formula V = (1/3)πr²h, where V represents the volume, π is a mathematical constant (approximately 3.14159), r is the radius, and h is the height of the cone.
2. Calculate the initial volume of the cone:
Let's assume the initial radius of the cone is r and the initial height is h. Using the volume formula, we can calculate the initial volume as V1 = (1/3)πr²h.
3. Calculate the increased radius and height:
Since both the radius and height are increased by 10%, we can calculate the new values as follows:
- Increased radius: r + 10% of r = r + 0.1r = 1.1r
- Increased height: h + 10% of h = h + 0.1h = 1.1h
4. Calculate the increased volume of the cone:
After obtaining the increased radius (1.1r) and height (1.1h), we can calculate the new volume using the volume formula:
V2 = (1/3)π(1.1r)²(1.1h)
5. Calculate the percentage increase in volume:
To find the percentage increase in volume, we need to compare the initial volume (V1) with the increased volume (V2). The percentage increase can be calculated using the formula:
Percentage Increase = ((V2 - V1) / V1) * 100
Example:
Let's consider an example to illustrate the calculation. Suppose the initial radius (r) of a cone is 5 units and the initial height (h) is 8 units.
1. Calculate the initial volume:
V1 = (1/3)π(5)²(8) = (1/3)π(25)(8) ≈ 209.44 cubic units
2. Calculate the increased radius and height:
Increased radius = 5 + 0.1(5) = 5 + 0.5 = 5.5 units
Increased height = 8 + 0.1(8) = 8 + 0.8 = 8.8 units
3. Calculate the increased volume:
V2 = (1/3)π(5.5)²(8.8) ≈ 266.71 cubic units
4. Calculate the percentage increase in volume:
Percentage Increase = ((266.71 - 209.44) / 209.44) * 100 ≈ 27.37%
Conclusion:
When both the radius and height of a cone are increased by 10%, the volume of the cone increases by approximately 27.37%.
Attention Class 9 Students!
To make sure you are not studying endlessly, EduRev has designed Class 9 study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Class 9.

|
Explore Courses for Class 9 exam
|

|
Similar Class 9 Doubts
If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ?
Question Description
If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ?.
If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ? for Class 9 2024 is part of Class 9 preparation. The Question and answers have been prepared according to the Class 9 exam syllabus. Information about If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ? covers all topics & solutions for Class 9 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ?.
Solutions for If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ? in English & in Hindi are available as part of our courses for Class 9.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here you can find the meaning of If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ? defined & explained in the simplest way possible. Besides giving the explanation of
If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ?, a detailed solution for If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ? has been provided alongside types of If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ? theory, EduRev gives you an
ample number of questions to practice If the radius and height of a cone both are increased by 10% then the volume of the cone is increased by how much ? tests, examples and also practice Class 9 tests.

|
Explore Courses for Class 9 exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























