Banking Exams Exam > Banking Exams Questions > Direction: Given below are two quantities na...
Start Learning for Free
Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.
Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?
Quantity B: 45 litres
- a)Quantity A > Quantity B
- b)Quantity A < quantity="" />
- c)Quantity A ≥ Quantity B
- d)Quantity A ≤ Quantity B
- e)Quantity A = Quantity B or No relation.
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
Direction: Given below are two quantities named A and B. Based on the...
Given:
Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water.
Quantity B: 45 liters
To determine:
The relation between Quantity A and Quantity B.
Solution:
To solve this problem, we need to find out how much water should be added to the mixture in Quantity A so that the final mixture has a water content of 50%.
Let's solve Quantity A step by step.
Step 1: Calculate the initial amount of water in the mixture.
The mixture in Quantity A contains 20% water, which means that 20% of 90 liters is water.
Water content in Quantity A = 20% of 90 liters = (20/100) * 90 liters = 18 liters.
Step 2: Calculate the amount of spirit in the mixture.
The remaining part of the mixture is spirit.
Spirit content in Quantity A = Total mixture - Water content = 90 liters - 18 liters = 72 liters.
Step 3: Calculate the final volume of the mixture after adding water.
Let's assume the final volume of the mixture is 'x' liters.
Since the final water content should be 50%, the amount of water in the final mixture will be 50% of 'x' liters.
Water content in the final mixture = 50% of 'x' liters = (50/100) * x liters = 0.5x liters.
The amount of spirit in the final mixture will be the remaining part.
Spirit content in the final mixture = Total mixture - Water content = 'x' liters - 0.5x liters = 0.5x liters.
Step 4: Set up an equation to find the value of 'x'.
According to the information given, the initial amount of spirit (72 liters) and the final amount of spirit (0.5x liters) should be the same.
So, we can set up the equation:
72 liters = 0.5x liters
Step 5: Solve the equation to find the value of 'x'.
Divide both sides of the equation by 0.5:
72 liters / 0.5 = x liters
144 liters = x liters
Therefore, the final volume of the mixture after adding water should be 144 liters.
Conclusion:
Quantity A represents the final volume of the mixture after adding water, which is 144 liters.
Quantity B represents the volume of the mixture, which is 45 liters.
Since Quantity A (144 liters) is greater than Quantity B (45 liters), the correct answer is option 'A' - Quantity A is greater than Quantity B.
Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water.
Quantity B: 45 liters
To determine:
The relation between Quantity A and Quantity B.
Solution:
To solve this problem, we need to find out how much water should be added to the mixture in Quantity A so that the final mixture has a water content of 50%.
Let's solve Quantity A step by step.
Step 1: Calculate the initial amount of water in the mixture.
The mixture in Quantity A contains 20% water, which means that 20% of 90 liters is water.
Water content in Quantity A = 20% of 90 liters = (20/100) * 90 liters = 18 liters.
Step 2: Calculate the amount of spirit in the mixture.
The remaining part of the mixture is spirit.
Spirit content in Quantity A = Total mixture - Water content = 90 liters - 18 liters = 72 liters.
Step 3: Calculate the final volume of the mixture after adding water.
Let's assume the final volume of the mixture is 'x' liters.
Since the final water content should be 50%, the amount of water in the final mixture will be 50% of 'x' liters.
Water content in the final mixture = 50% of 'x' liters = (50/100) * x liters = 0.5x liters.
The amount of spirit in the final mixture will be the remaining part.
Spirit content in the final mixture = Total mixture - Water content = 'x' liters - 0.5x liters = 0.5x liters.
Step 4: Set up an equation to find the value of 'x'.
According to the information given, the initial amount of spirit (72 liters) and the final amount of spirit (0.5x liters) should be the same.
So, we can set up the equation:
72 liters = 0.5x liters
Step 5: Solve the equation to find the value of 'x'.
Divide both sides of the equation by 0.5:
72 liters / 0.5 = x liters
144 liters = x liters
Therefore, the final volume of the mixture after adding water should be 144 liters.
Conclusion:
Quantity A represents the final volume of the mixture after adding water, which is 144 liters.
Quantity B represents the volume of the mixture, which is 45 liters.
Since Quantity A (144 liters) is greater than Quantity B (45 liters), the correct answer is option 'A' - Quantity A is greater than Quantity B.
Free Test
FREE
| Start Free Test |
Community Answer
Direction: Given below are two quantities named A and B. Based on the...
Quantity AGiven that, mixture of 90 litres of the spirit and water contains 20% water.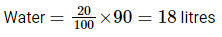
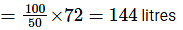
In the first mixture
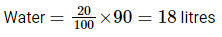
∴ Spirit = 90 – 18 = 72 litres
After adding some water to the mixture, water became 50% of the new mixture
∴ 72 litres of water in new mixture = 50% of new mixture
∴ Total litres of new mixture
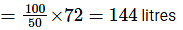
So, water to be added = 144 – 90 = 54 litres
Quantity B: 45 litres
∴ Quantity A > Quantity B
Hence, the correct option is (A).
Attention Banking Exams Students!
To make sure you are not studying endlessly, EduRev has designed Banking Exams study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Banking Exams.
|
Explore Courses for Banking Exams exam
|
|
Similar Banking Exams Doubts
Top Courses for Banking ExamsView all
Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer?
Question Description
Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer? for Banking Exams 2024 is part of Banking Exams preparation. The Question and answers have been prepared according to the Banking Exams exam syllabus. Information about Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Banking Exams 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer?.
Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer? for Banking Exams 2024 is part of Banking Exams preparation. The Question and answers have been prepared according to the Banking Exams exam syllabus. Information about Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Banking Exams 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer?.
Solutions for Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Banking Exams.
Download more important topics, notes, lectures and mock test series for Banking Exams Exam by signing up for free.
Here you can find the meaning of Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer?, a detailed solution for Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Direction: Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.Quantity A: A mixture of spirit and water measure 90 liters. It contains 20% water. How much water should be added to it so that water may be 50%?Quantity B: 45 litresa)Quantity A > Quantity Bb)Quantity A c)Quantity A ≥ Quantity Bd)Quantity A ≤ Quantity Be)Quantity A = Quantity B or No relation.Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice Banking Exams tests.
|
|
Explore Courses for Banking Exams exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup