Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > If f (z) is an analytic function whose modulu...
Start Learning for Free
If f (z) is an analytic function whose modulus is constant, then f (z) is a
- a)Function of z
- b)Constant
- c)Function whose only imaginary part is constant
- d)Function whose only real part is constant
Correct answer is option 'B'. Can you explain this answer?
Most Upvoted Answer
If f (z) is an analytic function whose modulus is constant, then f (z)...
Concept:
Let f(z) = u + iv be the analytic function,
then According to Cauchy-Riemann Equations
ux = vy & uy = - vx
Calculation:
Given:
modulus is constant
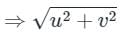 = k ⇒ u2 + v2 = k
= k ⇒ u2 + v2 = k
Now differentiating both sides w.r.t x and y, we get
2uux + 2vvx = 0 ⇒ 2uux = -2vvx --- (1)
2uuy + 2vvy = 0 ⇒ 2uuy = -2vvy --- (2)
Now applying Cauchy-Riemann Equations ux = vy & uy = - vx
2uux – 2vuy = 0 ⇒ 2uux = 2vuy --- (3)
2uuy + 2vux = 0 ⇒ 2uuy = -2vux --- (4)
Now dividing equations 3 and 4, we get
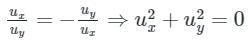
⇒ ux = uy = 0 ⇒ u is a constant function.
Similarly, we will get v is a constant function.
∴ f(z) is a constant function.
Let f(z) = u + iv be the analytic function,
then According to Cauchy-Riemann Equations
ux = vy & uy = - vx
Calculation:
Given:
modulus is constant
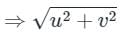 = k ⇒ u2 + v2 = k
= k ⇒ u2 + v2 = kNow differentiating both sides w.r.t x and y, we get
2uux + 2vvx = 0 ⇒ 2uux = -2vvx --- (1)
2uuy + 2vvy = 0 ⇒ 2uuy = -2vvy --- (2)
Now applying Cauchy-Riemann Equations ux = vy & uy = - vx
2uux – 2vuy = 0 ⇒ 2uux = 2vuy --- (3)
2uuy + 2vux = 0 ⇒ 2uuy = -2vux --- (4)
Now dividing equations 3 and 4, we get
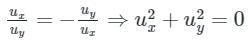
⇒ ux = uy = 0 ⇒ u is a constant function.
Similarly, we will get v is a constant function.
∴ f(z) is a constant function.
Free Test
FREE
| Start Free Test |
Community Answer
If f (z) is an analytic function whose modulus is constant, then f (z)...
Analyzing the given options:
To understand why option B is the correct answer, let's analyze the given options:
a) Function of z: This option suggests that the function f(z) is a function of z, which means it depends on the complex variable z itself. However, the given information states that the modulus of f(z) is constant, which means that the function does not depend on the specific values of z but only on their magnitudes. Therefore, this option is not correct.
b) Constant: This option suggests that the function f(z) is a constant function, meaning it does not depend on z at all. Since the modulus of f(z) is constant, it implies that the function has a constant magnitude and does not vary with z. Therefore, this option is correct.
c) Function whose only imaginary part is constant: This option suggests that the function f(z) has a constant imaginary part but may have a non-constant real part. However, the given information states that the modulus of f(z) is constant, which means that both the real and imaginary parts must be constant. Therefore, this option is not correct.
d) Function whose only real part is constant: This option suggests that the function f(z) has a constant real part but may have a non-constant imaginary part. However, the given information states that the modulus of f(z) is constant, which means that both the real and imaginary parts must be constant. Therefore, this option is not correct.
Understanding the concept:
In complex analysis, a function is said to be analytic if it is differentiable at every point within its domain. The Cauchy-Riemann equations provide necessary and sufficient conditions for a function to be analytic.
For a function f(z) to have a constant modulus, it means that |f(z)| = constant for all values of z in its domain. Geometrically, this represents a set of points on the complex plane that lie on a circle or a straight line.
Why option B is correct:
If the modulus of f(z) is constant, it implies that the function maps every point in its domain to a fixed distance from the origin on the complex plane. This means that the function does not change its magnitude as z varies.
Since the magnitude of a complex number is determined by both its real and imaginary parts, for the modulus to be constant, both the real and imaginary parts of f(z) must be constant. Therefore, the correct answer is option B: Constant.
Conclusion:
In summary, if f(z) is an analytic function whose modulus is constant, then the function must be a constant function, meaning it does not depend on the variable z. Both the real and imaginary parts of f(z) must be constant for the modulus to remain constant.
To understand why option B is the correct answer, let's analyze the given options:
a) Function of z: This option suggests that the function f(z) is a function of z, which means it depends on the complex variable z itself. However, the given information states that the modulus of f(z) is constant, which means that the function does not depend on the specific values of z but only on their magnitudes. Therefore, this option is not correct.
b) Constant: This option suggests that the function f(z) is a constant function, meaning it does not depend on z at all. Since the modulus of f(z) is constant, it implies that the function has a constant magnitude and does not vary with z. Therefore, this option is correct.
c) Function whose only imaginary part is constant: This option suggests that the function f(z) has a constant imaginary part but may have a non-constant real part. However, the given information states that the modulus of f(z) is constant, which means that both the real and imaginary parts must be constant. Therefore, this option is not correct.
d) Function whose only real part is constant: This option suggests that the function f(z) has a constant real part but may have a non-constant imaginary part. However, the given information states that the modulus of f(z) is constant, which means that both the real and imaginary parts must be constant. Therefore, this option is not correct.
Understanding the concept:
In complex analysis, a function is said to be analytic if it is differentiable at every point within its domain. The Cauchy-Riemann equations provide necessary and sufficient conditions for a function to be analytic.
For a function f(z) to have a constant modulus, it means that |f(z)| = constant for all values of z in its domain. Geometrically, this represents a set of points on the complex plane that lie on a circle or a straight line.
Why option B is correct:
If the modulus of f(z) is constant, it implies that the function maps every point in its domain to a fixed distance from the origin on the complex plane. This means that the function does not change its magnitude as z varies.
Since the magnitude of a complex number is determined by both its real and imaginary parts, for the modulus to be constant, both the real and imaginary parts of f(z) must be constant. Therefore, the correct answer is option B: Constant.
Conclusion:
In summary, if f(z) is an analytic function whose modulus is constant, then the function must be a constant function, meaning it does not depend on the variable z. Both the real and imaginary parts of f(z) must be constant for the modulus to remain constant.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer?.
If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer?.
Solutions for If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If f (z) is an analytic function whose modulus is constant, then f (z) is aa)Function of zb)Constantc)Function whose only imaginary part is constantd)Function whose only real part is constantCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























