Electrical Engineering (EE) Exam > Electrical Engineering (EE) Questions > The impulse response of an RL circuit is:a)Pa...
Start Learning for Free
The impulse response of an RL circuit is:
- a)Parabolic function
- b)Step function
- c)Rising exponential function
- d)Decaying exponential function
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
The impulse response of an RL circuit is:a)Parabolic functionb)Step fu...
The impulse response of an RL circuit refers to the output response of the circuit when an impulse signal is applied to it. An impulse signal is a short pulse with an infinite amplitude and infinitesimal duration. When this impulse signal is applied to an RL circuit, the circuit responds by generating a specific output waveform, which is known as the impulse response.
RL Circuit:
Before diving into the impulse response, let's first understand the RL circuit. An RL circuit consists of a resistor (R) and an inductor (L) connected in series or parallel. When a voltage or current is applied to the circuit, it takes some time for the current to reach its steady-state value due to the presence of inductance.
Impulse Response:
The impulse response of an RL circuit is a measure of how the circuit responds to an impulse input. It describes the behavior of the circuit over time. The impulse response may vary depending on the initial conditions of the circuit.
Decaying Exponential Function:
The correct answer is option 'D', which states that the impulse response of an RL circuit is a decaying exponential function. This means that the output waveform of the RL circuit, when an impulse signal is applied, decays over time in an exponential manner.
Explanation:
When an impulse signal is applied to an RL circuit, the inductor resists the sudden change in current. As a result, the current through the inductor increases gradually until it reaches its steady-state value. This behavior can be described by a decaying exponential function.
The decaying exponential function represents the time it takes for the inductor to reach its steady-state value. Initially, the current rises rapidly, but as time passes, the rate of change decreases, and the current approaches a constant value. This behavior is characteristic of RL circuits due to the presence of inductance.
The decaying exponential function can be mathematically represented as:
i(t) = I0 * e^(-t/τ)
where i(t) is the current at time t, I0 is the initial current, t is the time, and τ is the time constant of the circuit. The time constant depends on the values of resistance and inductance in the circuit.
In summary, the impulse response of an RL circuit is a decaying exponential function because the circuit takes time to reach its steady-state value due to the presence of inductance. The decaying exponential function represents the gradual increase in current until it reaches a constant value.
RL Circuit:
Before diving into the impulse response, let's first understand the RL circuit. An RL circuit consists of a resistor (R) and an inductor (L) connected in series or parallel. When a voltage or current is applied to the circuit, it takes some time for the current to reach its steady-state value due to the presence of inductance.
Impulse Response:
The impulse response of an RL circuit is a measure of how the circuit responds to an impulse input. It describes the behavior of the circuit over time. The impulse response may vary depending on the initial conditions of the circuit.
Decaying Exponential Function:
The correct answer is option 'D', which states that the impulse response of an RL circuit is a decaying exponential function. This means that the output waveform of the RL circuit, when an impulse signal is applied, decays over time in an exponential manner.
Explanation:
When an impulse signal is applied to an RL circuit, the inductor resists the sudden change in current. As a result, the current through the inductor increases gradually until it reaches its steady-state value. This behavior can be described by a decaying exponential function.
The decaying exponential function represents the time it takes for the inductor to reach its steady-state value. Initially, the current rises rapidly, but as time passes, the rate of change decreases, and the current approaches a constant value. This behavior is characteristic of RL circuits due to the presence of inductance.
The decaying exponential function can be mathematically represented as:
i(t) = I0 * e^(-t/τ)
where i(t) is the current at time t, I0 is the initial current, t is the time, and τ is the time constant of the circuit. The time constant depends on the values of resistance and inductance in the circuit.
In summary, the impulse response of an RL circuit is a decaying exponential function because the circuit takes time to reach its steady-state value due to the presence of inductance. The decaying exponential function represents the gradual increase in current until it reaches a constant value.
Free Test
FREE
| Start Free Test |
Community Answer
The impulse response of an RL circuit is:a)Parabolic functionb)Step fu...
The RL circuit comprises of the resistor and inductor connected in series.
The equation can be written as:
The equation can be written as:
1 = RI(s) + sLI(s)
1 = I(s) [R + sL]
I(s) = 1 / (R +sL)
Taking the inverse Laplace, we get:
1 = I(s) [R + sL]
I(s) = 1 / (R +sL)
Taking the inverse Laplace, we get:
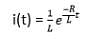
The equation clearly depicts that the impulse response is a decaying exponential function.
Hence, the correct answer is option (d).
Attention Electrical Engineering (EE) Students!
To make sure you are not studying endlessly, EduRev has designed Electrical Engineering (EE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Electrical Engineering (EE).

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Similar Electrical Engineering (EE) Doubts
The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer?
Question Description
The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer? for Electrical Engineering (EE) 2024 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer?.
The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer? for Electrical Engineering (EE) 2024 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electrical Engineering (EE).
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Here you can find the meaning of The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The impulse response of an RL circuit is:a)Parabolic functionb)Step functionc)Rising exponential functiond)Decaying exponential functionCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Electrical Engineering (EE) tests.

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.