Electrical Engineering (EE) Exam > Electrical Engineering (EE) Questions > Diagonal elements and off-diagonal elements o...
Start Learning for Free
Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known as
- a)self-admittances and mutual admittances
- b)mutual admittances and self-admittances
- c)self-admittances
- d)mutual admittances
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
Diagonal elements and off-diagonal elements of the bus admittance matr...
Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known as:
The diagonal elements and off-diagonal elements of the bus admittance matrix in power system analysis are known as self-admittances and mutual admittances, respectively.
Explanation:
In power system analysis, the bus admittance matrix is used to represent the network of interconnected buses in an electrical power system. It is a complex symmetric matrix that describes the electrical relationships between the buses in terms of their admittances.
The diagonal elements of the bus admittance matrix represent the self-admittances of the buses. These elements correspond to the admittance of each individual bus with respect to itself. In other words, they represent the self-impedance or self-admittance of each bus without considering the influence of other buses. The self-admittances are usually given by the sum of the shunt conductances and susceptances connected to each bus.
On the other hand, the off-diagonal elements of the bus admittance matrix represent the mutual admittances between pairs of buses. These elements correspond to the admittance between two different buses in the network. They represent the coupling or interaction between different buses in the system. The mutual admittances are usually given by the sum of the series conductances and susceptances between pairs of buses.
Summary:
To summarize, the diagonal elements of the bus admittance matrix are known as self-admittances because they represent the admittance of each bus with respect to itself. The off-diagonal elements of the bus admittance matrix are known as mutual admittances because they represent the admittance between pairs of different buses in the system.
The diagonal elements and off-diagonal elements of the bus admittance matrix in power system analysis are known as self-admittances and mutual admittances, respectively.
Explanation:
In power system analysis, the bus admittance matrix is used to represent the network of interconnected buses in an electrical power system. It is a complex symmetric matrix that describes the electrical relationships between the buses in terms of their admittances.
The diagonal elements of the bus admittance matrix represent the self-admittances of the buses. These elements correspond to the admittance of each individual bus with respect to itself. In other words, they represent the self-impedance or self-admittance of each bus without considering the influence of other buses. The self-admittances are usually given by the sum of the shunt conductances and susceptances connected to each bus.
On the other hand, the off-diagonal elements of the bus admittance matrix represent the mutual admittances between pairs of buses. These elements correspond to the admittance between two different buses in the network. They represent the coupling or interaction between different buses in the system. The mutual admittances are usually given by the sum of the series conductances and susceptances between pairs of buses.
Summary:
To summarize, the diagonal elements of the bus admittance matrix are known as self-admittances because they represent the admittance of each bus with respect to itself. The off-diagonal elements of the bus admittance matrix are known as mutual admittances because they represent the admittance between pairs of different buses in the system.
Free Test
FREE
| Start Free Test |
Community Answer
Diagonal elements and off-diagonal elements of the bus admittance matr...
Bus Admittance Matrix:
- In a power system, Bus Admittance Matrix represents the nodal admittances of the various buses.
- Admittance matrix is used to analyze the data that is needed in the load or a power flow study of the buses.
- It explains the admittance and the topology of the network.
The following are the advantages of the bus admittance matrix.
- The data preparation of the bus admittance matrix is very simple.
- The formation of the bus admittance matrix and their modification is easy.
- The bus admittance matrix is a sparse matrix as most of the elements are zero and hence the memory require requirement to store the network data is less. Hence it is preferred to develop the equations for load flow studies.
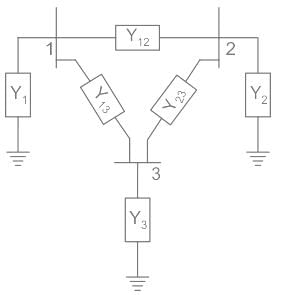
For the above figure, the admittance matrix is as shown below.
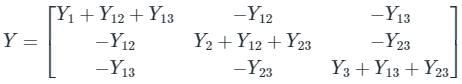
- Diagonal elements of the Bus Admittance matrix are known as self-admittances and the off-diagonal elements are known as mutual admittances.
- The diagonal element Yii is the sum of all the admittances of the elements connected to the ith bus.
- Yii = Σ yik , k = 1, 2, …n and k ≠ i
- The off-diagonal element Yij is equal to the minus of the admittance of the element connected between buses i and j.
- Yij = -yij
Some observations on the admittance matrix:
- Admittance matrix is a sparse matrix
- Diagonal elements are dominating
- Off diagonal elements are symmetric in terms of both position and value with respect to diagonal.
- The diagonal element of each node is the sum of the admittances connected to it
- Off diagonal element is negated admittance

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Question Description
Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer?.
Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electrical Engineering (EE).
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Here you can find the meaning of Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Diagonal elements and off-diagonal elements of the bus admittance matrix are respectively known asa)self-admittances and mutual admittancesb)mutual admittances and self-admittancesc)self-admittancesd)mutual admittancesCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Electrical Engineering (EE) tests.

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























