GATE Exam > GATE Questions > An analog voltage in the range 0 to 5V is div...
Start Learning for Free
An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -
- a)5
- b)10
- c)0.25
- d)4
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
An analog voltage in the range 0 to 5V is divided into 10 equal interv...
Concept:
Maximum Quantization error = 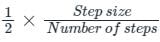
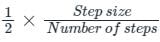
Step size= (Vmax - Vmin)
Calculation:
Given
Analog voltage ranging from 0 V (Vmin) to 5 V (Vmax)
No. of interval or number of steps = 10
Step size = (5 - 0) = 5 V
Maximum quantization error = 1/2 × (5/10) = 0.25 V
Free Test
FREE
| Start Free Test |
Community Answer
An analog voltage in the range 0 to 5V is divided into 10 equal interv...
Given:
- Analog voltage range: 0 to 5V
- Divided into 10 equal intervals
- Conversion into 4-bit digital output
To find:
- Maximum quantization error
Solution:
To understand the solution, we need to first understand the concept of quantization and quantization error.
Quantization:
Quantization is the process of converting a continuous range of values into a discrete set of levels. In this case, the analog voltage range of 0 to 5V is divided into 10 equal intervals, resulting in 11 possible discrete levels.
Quantization Error:
Quantization error is the difference between the original continuous value and the quantized value. It occurs because the quantized value can only represent one of the discrete levels and not the exact continuous value.
Calculation:
In this case, we have a 4-bit digital output, which means we can represent a maximum of 2^4 = 16 levels. However, we are dividing the analog voltage range into only 10 levels.
To calculate the maximum quantization error, we need to consider the worst-case scenario. In this case, the worst-case scenario would be when the actual analog voltage is at the boundary of two adjacent levels.
The size of each interval can be calculated as follows:
Interval size = (Maximum voltage - Minimum voltage) / Number of intervals
= (5V - 0V) / 10
= 0.5V
The maximum quantization error would occur when the actual analog voltage is at the boundary of two adjacent levels. So the maximum quantization error can be calculated as half of the interval size.
Maximum quantization error = Interval size / 2
= 0.5V / 2
= 0.25V
Therefore, the maximum quantization error is 0.25V, which corresponds to option 'c'.
- Analog voltage range: 0 to 5V
- Divided into 10 equal intervals
- Conversion into 4-bit digital output
To find:
- Maximum quantization error
Solution:
To understand the solution, we need to first understand the concept of quantization and quantization error.
Quantization:
Quantization is the process of converting a continuous range of values into a discrete set of levels. In this case, the analog voltage range of 0 to 5V is divided into 10 equal intervals, resulting in 11 possible discrete levels.
Quantization Error:
Quantization error is the difference between the original continuous value and the quantized value. It occurs because the quantized value can only represent one of the discrete levels and not the exact continuous value.
Calculation:
In this case, we have a 4-bit digital output, which means we can represent a maximum of 2^4 = 16 levels. However, we are dividing the analog voltage range into only 10 levels.
To calculate the maximum quantization error, we need to consider the worst-case scenario. In this case, the worst-case scenario would be when the actual analog voltage is at the boundary of two adjacent levels.
The size of each interval can be calculated as follows:
Interval size = (Maximum voltage - Minimum voltage) / Number of intervals
= (5V - 0V) / 10
= 0.5V
The maximum quantization error would occur when the actual analog voltage is at the boundary of two adjacent levels. So the maximum quantization error can be calculated as half of the interval size.
Maximum quantization error = Interval size / 2
= 0.5V / 2
= 0.25V
Therefore, the maximum quantization error is 0.25V, which corresponds to option 'c'.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
Question Description
An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer? for GATE 2025 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer?.
An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer? for GATE 2025 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer?.
Solutions for An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer?, a detailed solution for An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An analog voltage in the range 0 to 5V is divided into 10 equal intervals for conversion into 4 bit digital output. The maximum quantization error (in V) is -a)5b)10c)0.25d)4Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.





















