Electrical Engineering (EE) Exam > Electrical Engineering (EE) Questions > The most important technique used for stabili...
Start Learning for Free
The most important technique used for stability and the transient response of the system is
- a)Nyquist plot
- b)Root locus
- c)Bode plot
- d)Routh Hurwitz criteria
Correct answer is option 'B'. Can you explain this answer?
Most Upvoted Answer
The most important technique used for stability and the transient resp...
Definition:
The root locus plots the poles of the closed-loop transfer function in the complex s-plane as K varies from 0 to ∞
The purpose of Root locus is defined as:
- To find the nature of the system and ‘K’ value for stability.
- To find the relative stability.
- If the root locus branches move towards the right, system is less stable and if they move towards the left then the system is more relative stable.
- It is the best method to find the Relative stability and RH criteria is best to find absolute stability
The relation between the closed-loop and open-loop poles
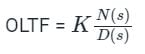
D(s) = 0 gives open-loop poles and N(s) = 0 gives closed-loop poles
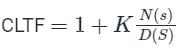
Characteristic equation is D(s) + kN(s) = 0.
Closed-loop poles are nothing but the sum of open-loop poles and zeroes.
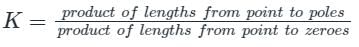
Free Test
FREE
| Start Free Test |
Community Answer
The most important technique used for stability and the transient resp...
Root Locus:
Explanation:
The root locus method is a powerful tool used in control systems engineering to analyze the transient response and stability of a system. It is based on the concept of the poles of the closed-loop transfer function as a parameter, such as the gain of a proportional controller, is varied.
Key Points:
- The root locus technique provides insights into how the poles of the closed-loop system move as a certain parameter is changed.
- By plotting the roots of the characteristic equation in the complex plane as the parameter varies, engineers can determine the stability and transient response of the system.
- The root locus plot helps in designing controllers that meet specific performance criteria such as settling time, overshoot, and steady-state error.
- It is a graphical method that can be used to analyze the effects of adding poles and zeros to the system as well as changing the controller parameters.
- By examining the root locus plot, engineers can determine the range of controller parameters that will result in a stable system with acceptable transient response characteristics.
Conclusion:
In conclusion, the root locus technique is crucial for analyzing the stability and transient response of a control system. By using this method, engineers can design controllers that meet desired performance specifications and ensure the system operates effectively.
Explanation:
The root locus method is a powerful tool used in control systems engineering to analyze the transient response and stability of a system. It is based on the concept of the poles of the closed-loop transfer function as a parameter, such as the gain of a proportional controller, is varied.
Key Points:
- The root locus technique provides insights into how the poles of the closed-loop system move as a certain parameter is changed.
- By plotting the roots of the characteristic equation in the complex plane as the parameter varies, engineers can determine the stability and transient response of the system.
- The root locus plot helps in designing controllers that meet specific performance criteria such as settling time, overshoot, and steady-state error.
- It is a graphical method that can be used to analyze the effects of adding poles and zeros to the system as well as changing the controller parameters.
- By examining the root locus plot, engineers can determine the range of controller parameters that will result in a stable system with acceptable transient response characteristics.
Conclusion:
In conclusion, the root locus technique is crucial for analyzing the stability and transient response of a control system. By using this method, engineers can design controllers that meet desired performance specifications and ensure the system operates effectively.
|
Explore Courses for Electrical Engineering (EE) exam
|
|
Top Courses for Electrical Engineering (EE)View all
Question Description
The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer?.
The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer? for Electrical Engineering (EE) 2025 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer?.
Solutions for The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electrical Engineering (EE).
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Here you can find the meaning of The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The most important technique used for stability and the transient response of the system isa)Nyquist plotb)Root locusc)Bode plotd)Routh Hurwitz criteriaCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Electrical Engineering (EE) tests.
|
|
Explore Courses for Electrical Engineering (EE) exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup