Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > Trapezoidal Rule gives exact value of the int...
Start Learning for Free
Trapezoidal Rule gives exact value of the integral when the integrand is a
- a)linear function
- b)quadratic function
- c)cubic function
- d)polynomial of any degree
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
Trapezoidal Rule gives exact value of the integral when the integrand ...
Introduction:
The Trapezoidal Rule is a numerical integration method that approximates the definite integral of a function by dividing the area under the curve into trapezoids. This method is simple to implement and provides a good approximation for smooth functions.
Explanation:
The Trapezoidal Rule can give an exact value of the integral when the integrand is a linear function. In this case, the function can be represented by a straight line, and the area under the curve can be accurately calculated using the trapezoidal approximation.
Reasoning:
The Trapezoidal Rule approximates the area under the curve by dividing it into trapezoids. Each trapezoid is formed by connecting two adjacent points on the curve with a straight line segment. The area of each trapezoid is then calculated by taking the average of the heights of the two adjacent points and multiplying it by the width of the trapezoid.
When the integrand is a linear function, the curve is a straight line. In this case, the Trapezoidal Rule accurately approximates the area under the curve by dividing it into trapezoids with equal widths. Since the function is linear, the heights of the trapezoids remain constant throughout the interval, and the trapezoidal approximation becomes exact.
Example:
Let's consider the linear function f(x) = 2x + 3 over the interval [1, 5]. Using the Trapezoidal Rule, we divide the interval into n subintervals and approximate the integral as follows:
∫[1, 5] (2x + 3) dx ≈ Δx/2 * [f(x0) + 2f(x1) + 2f(x2) + ... + 2f(xn-1) + f(xn)]
where Δx = (b - a)/n is the width of each subinterval, x0 = 1, xn = 5, and xi = a + iΔx.
Since the integrand is a linear function, the function values f(xi) = 2xi + 3 remain constant throughout the interval. Therefore, the Trapezoidal Rule becomes exact, and the approximation becomes the exact value of the integral.
Conclusion:
The Trapezoidal Rule gives an exact value of the integral when the integrand is a linear function. This is because the Trapezoidal Rule accurately approximates the area under the curve by dividing it into trapezoids with equal widths. For linear functions, the heights of the trapezoids remain constant, resulting in an exact approximation of the integral.
The Trapezoidal Rule is a numerical integration method that approximates the definite integral of a function by dividing the area under the curve into trapezoids. This method is simple to implement and provides a good approximation for smooth functions.
Explanation:
The Trapezoidal Rule can give an exact value of the integral when the integrand is a linear function. In this case, the function can be represented by a straight line, and the area under the curve can be accurately calculated using the trapezoidal approximation.
Reasoning:
The Trapezoidal Rule approximates the area under the curve by dividing it into trapezoids. Each trapezoid is formed by connecting two adjacent points on the curve with a straight line segment. The area of each trapezoid is then calculated by taking the average of the heights of the two adjacent points and multiplying it by the width of the trapezoid.
When the integrand is a linear function, the curve is a straight line. In this case, the Trapezoidal Rule accurately approximates the area under the curve by dividing it into trapezoids with equal widths. Since the function is linear, the heights of the trapezoids remain constant throughout the interval, and the trapezoidal approximation becomes exact.
Example:
Let's consider the linear function f(x) = 2x + 3 over the interval [1, 5]. Using the Trapezoidal Rule, we divide the interval into n subintervals and approximate the integral as follows:
∫[1, 5] (2x + 3) dx ≈ Δx/2 * [f(x0) + 2f(x1) + 2f(x2) + ... + 2f(xn-1) + f(xn)]
where Δx = (b - a)/n is the width of each subinterval, x0 = 1, xn = 5, and xi = a + iΔx.
Since the integrand is a linear function, the function values f(xi) = 2xi + 3 remain constant throughout the interval. Therefore, the Trapezoidal Rule becomes exact, and the approximation becomes the exact value of the integral.
Conclusion:
The Trapezoidal Rule gives an exact value of the integral when the integrand is a linear function. This is because the Trapezoidal Rule accurately approximates the area under the curve by dividing it into trapezoids with equal widths. For linear functions, the heights of the trapezoids remain constant, resulting in an exact approximation of the integral.
Free Test
FREE
| Start Free Test |
Community Answer
Trapezoidal Rule gives exact value of the integral when the integrand ...
Trapezoidal rule
It integrates a linear function exactly and produces errors for polynomial functions of degree 2 or higher.
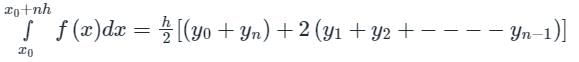
Here, the interval is divided into 'n' number of intervals (even or odd) of equal width 'h' b is the upper limit, a is the lower limit, h is the step size
It fits for a 1-degree (linear) polynomial.
According to Simpson's 1/3 rule:
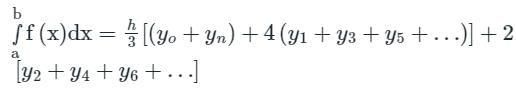
It fits for 2-degree (quadratic) polynomial.
According to Simpson's 3/8 rule
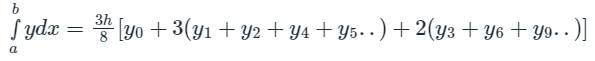
It fits for 3-degree (cubic) polynomial.
It integrates a linear function exactly and produces errors for polynomial functions of degree 2 or higher.
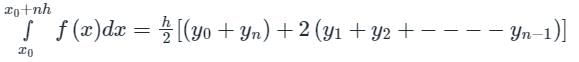
Here, the interval is divided into 'n' number of intervals (even or odd) of equal width 'h' b is the upper limit, a is the lower limit, h is the step size
It fits for a 1-degree (linear) polynomial.
According to Simpson's 1/3 rule:
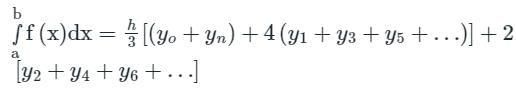
It fits for 2-degree (quadratic) polynomial.
According to Simpson's 3/8 rule
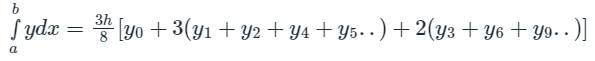
It fits for 3-degree (cubic) polynomial.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer?.
Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Trapezoidal Rule gives exact value of the integral when the integrand is aa)linear functionb)quadratic functionc)cubic functiond)polynomial of any degreeCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























