Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > The minimum number of colours that is suffici...
Start Learning for Free
The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.
Correct answer is '4'. Can you explain this answer?
Most Upvoted Answer
The minimum number of colours that is sufficient to vertex-colour any ...
According to the property of planar graph and four colour theorems. Maximum number of colours that are needed to vertex-colour any planar graph is 4.
Example:
In this graph, only 3 colours are enough to colour this planar graph.
In this graph, only 3 colours are enough to colour this planar graph.
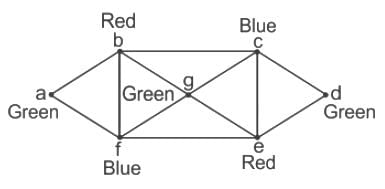
But if in this graph, there is an edge from a to d also, then three colours are not enough to vertex-colour this graph.
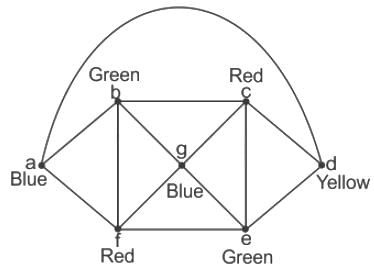
In this graph, 4 colours are needed to vertex- colour this graph.
Free Test
FREE
| Start Free Test |
Community Answer
The minimum number of colours that is sufficient to vertex-colour any ...
Minimum Number of Colors for Planar Graphs
Planar graphs are graphs that can be drawn on a plane without any edges crossing each other. The Four Color Theorem states that any planar graph can be colored with no more than 4 colors in such a way that no two adjacent vertices have the same color.
Explanation
- The Four Color Theorem was first stated in 1852 and was finally proved in 1976 after significant advancements in graph theory.
- The proof involves a combination of computer-based verifications and mathematical arguments.
- The key idea behind the theorem is that any planar graph can be reduced to a simpler form known as a 3-connected planar graph, which can then be colored using 4 colors or fewer.
- By using a combination of induction, discharging arguments, and case analysis, mathematicians were able to show that 4 colors are always sufficient to color a planar graph.
Implications
- The Four Color Theorem has important implications in various areas such as map coloring, scheduling problems, and circuit design.
- It provides a simple and efficient method for coloring planar graphs, which are commonly encountered in real-world applications.
- Understanding the minimum number of colors required for planar graphs can lead to more efficient algorithms and solutions in various fields of study.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
Question Description
The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer?.
The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer?.
Solutions for The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer?, a detailed solution for The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer? has been provided alongside types of The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.Correct answer is '4'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.





















