Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Which of the following languages accept pumpi...
Start Learning for Free
Which of the following languages accept pumping lemma?
- a)Regular Languages
- b)Context Free Languages
- c)Recursive Languages
- d)Recursively Enumerable Languages
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
Which of the following languages accept pumping lemma?a)Regular Langua...
Explanation:
The Pumping Lemma is a theorem in formal language theory that provides a necessary condition for a language to be considered regular. It is used to prove that certain languages are not regular.
Regular Languages:
Regular languages are the languages that can be recognized by a finite automaton or expressed by a regular expression. They are closed under union, concatenation, and Kleene star operations. The Pumping Lemma can be used to prove that certain languages are not regular by showing that they do not satisfy the conditions of the lemma.
Context-Free Languages:
Context-free languages are a more general class of languages than regular languages. They can be recognized by a pushdown automaton and expressed by a context-free grammar. However, the Pumping Lemma does not apply to context-free languages. Instead, the pumping lemma for context-free languages is used to prove that certain languages are not context-free.
Recursive Languages:
Recursive languages, also known as decidable languages, are languages for which there exists a Turing machine that halts and accepts every string in the language and halts and rejects every string not in the language. The Pumping Lemma is not applicable to recursive languages because the Pumping Lemma is used to prove that certain languages are not regular, and recursive languages are a superset of regular languages.
Recursively Enumerable Languages:
Recursively enumerable languages, also known as recursively enumerable sets, are languages for which there exists a Turing machine that halts and accepts every string in the language, but may either halt and reject or loop indefinitely on strings not in the language. The Pumping Lemma is not applicable to recursively enumerable languages because the Pumping Lemma is used to prove that certain languages are not regular, and recursively enumerable languages are a superset of regular languages.
Therefore, the correct option is D) Recursively Enumerable Languages.
The Pumping Lemma is a theorem in formal language theory that provides a necessary condition for a language to be considered regular. It is used to prove that certain languages are not regular.
Regular Languages:
Regular languages are the languages that can be recognized by a finite automaton or expressed by a regular expression. They are closed under union, concatenation, and Kleene star operations. The Pumping Lemma can be used to prove that certain languages are not regular by showing that they do not satisfy the conditions of the lemma.
Context-Free Languages:
Context-free languages are a more general class of languages than regular languages. They can be recognized by a pushdown automaton and expressed by a context-free grammar. However, the Pumping Lemma does not apply to context-free languages. Instead, the pumping lemma for context-free languages is used to prove that certain languages are not context-free.
Recursive Languages:
Recursive languages, also known as decidable languages, are languages for which there exists a Turing machine that halts and accepts every string in the language and halts and rejects every string not in the language. The Pumping Lemma is not applicable to recursive languages because the Pumping Lemma is used to prove that certain languages are not regular, and recursive languages are a superset of regular languages.
Recursively Enumerable Languages:
Recursively enumerable languages, also known as recursively enumerable sets, are languages for which there exists a Turing machine that halts and accepts every string in the language, but may either halt and reject or loop indefinitely on strings not in the language. The Pumping Lemma is not applicable to recursively enumerable languages because the Pumping Lemma is used to prove that certain languages are not regular, and recursively enumerable languages are a superset of regular languages.
Therefore, the correct option is D) Recursively Enumerable Languages.
Free Test
FREE
| Start Free Test |
Community Answer
Which of the following languages accept pumping lemma?a)Regular Langua...
Pumping Lemma for Regular Languages: For any regular language L, if a string 'v' is pumped any number of times, it will still belong to the same language.
If L is a regular language, there exists an integer 'n' in which if all x∈L with |x|≥n, then there exists u,v,w∈Σ∗ such that x=uvw and it further follows the following conditions:
If L is a regular language, there exists an integer 'n' in which if all x∈L with |x|≥n, then there exists u,v,w∈Σ∗ such that x=uvw and it further follows the following conditions:
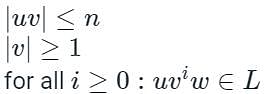
Pumping Lemma for Context-Free Languages: For any context-free language L, there exist two substrings that can be pumped any number of times and that string will still be following the same grammar.
If L is a context-free language, there exists an integer 'n' in which all x∈L with |x|≥n and there exists u,v,w,x,y∈Σ∗ such that x=uvwxy and it further follows the following conditions:
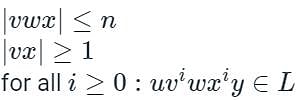
Recursive Languages: Recursive Languages do not follow the pumping lemma.
Recursively Enumerable Languages: Recursively Enumerable Languages do not follow the pumping lemma.
Attention Computer Science Engineering (CSE) Students!
To make sure you are not studying endlessly, EduRev has designed Computer Science Engineering (CSE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Computer Science Engineering (CSE).

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Similar Computer Science Engineering (CSE) Doubts
Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer?
Question Description
Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer?.
Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer?.
Solutions for Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following languages accept pumping lemma?a)Regular Languagesb)Context Free Languagesc)Recursive Languagesd)Recursively Enumerable LanguagesCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























