Mechanical Engineering Exam > Mechanical Engineering Questions > A solid cylindrical stainless steel work pie...
Start Learning for Free
A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2
- a)20.8 kN
- b)31 MN
- c)78.6 KN
- d)78.6 MN
Correct answer is option 'D'. Can you explain this answer?
Most Upvoted Answer
A solid cylindrical stainless steel work piece of 200 mm diameter and...
Question:
A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2
a)20.8 kN
b)31 MN
c)78.6 KN
d)78.6 MN
Answer:
To calculate the forging force required for the given problem, we need to follow the below steps:
Step 1: Calculate the original volume of the workpiece
Volume of original workpiece = π/4 × D² × H
Where D = 200 mm and H = 150 mm
Volume of original workpiece = π/4 × (200)² × (150) = 4,712,388.98 mm³
Step 2: Calculate the final volume of the workpiece
As per the problem statement, the height of the workpiece is reduced by 50%. So, the final height of the workpiece will be 75 mm.
Volume of final workpiece = π/4 × D² × H
Where D = 200 mm and H = 75 mm
Volume of final workpiece = π/4 × (200)² × (75) = 1,178,097.25 mm³
Step 3: Calculate the volume reduction
Volume reduction = Original volume - Final volume
Volume reduction = 4,712,388.98 - 1,178,097.25 = 3,534,291.73 mm³
Step 4: Calculate the forging force
Forging force = Flow stress × Volume reduction × (1 + Coefficient of friction)
Where, Flow stress = 1000 MPa
Volume reduction = 3,534,291.73 mm³
Coefficient of friction = 0.2
Forging force = 1000 × 10⁶ × 3,534,291.73 × (1 + 0.2) = 78,573,907.23 N
Therefore, the correct option is D) 78.6 MN.
Note: The answer is given in Newtons, but the options are in kilonewtons and meganewtons. We need to convert the answer to the appropriate unit before selecting the correct option. 1 MN = 1000 kN.
A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2
a)20.8 kN
b)31 MN
c)78.6 KN
d)78.6 MN
Answer:
To calculate the forging force required for the given problem, we need to follow the below steps:
Step 1: Calculate the original volume of the workpiece
Volume of original workpiece = π/4 × D² × H
Where D = 200 mm and H = 150 mm
Volume of original workpiece = π/4 × (200)² × (150) = 4,712,388.98 mm³
Step 2: Calculate the final volume of the workpiece
As per the problem statement, the height of the workpiece is reduced by 50%. So, the final height of the workpiece will be 75 mm.
Volume of final workpiece = π/4 × D² × H
Where D = 200 mm and H = 75 mm
Volume of final workpiece = π/4 × (200)² × (75) = 1,178,097.25 mm³
Step 3: Calculate the volume reduction
Volume reduction = Original volume - Final volume
Volume reduction = 4,712,388.98 - 1,178,097.25 = 3,534,291.73 mm³
Step 4: Calculate the forging force
Forging force = Flow stress × Volume reduction × (1 + Coefficient of friction)
Where, Flow stress = 1000 MPa
Volume reduction = 3,534,291.73 mm³
Coefficient of friction = 0.2
Forging force = 1000 × 10⁶ × 3,534,291.73 × (1 + 0.2) = 78,573,907.23 N
Therefore, the correct option is D) 78.6 MN.
Note: The answer is given in Newtons, but the options are in kilonewtons and meganewtons. We need to convert the answer to the appropriate unit before selecting the correct option. 1 MN = 1000 kN.
Free Test
FREE
| Start Free Test |
Community Answer
A solid cylindrical stainless steel work piece of 200 mm diameter and...
Given d0 = 200mm, h0 = 150mm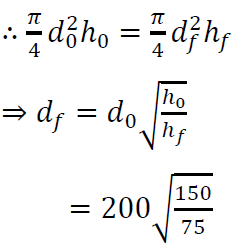
Hf = 0.5 * 150 = 75 mm
Since volume remains constant in forging,
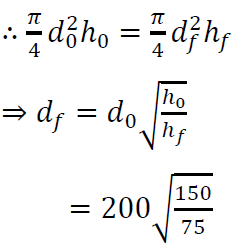
= 282.84 mm
Flow stress = σf - σy = 1000MPa
Μ = 0.2
Forging force, F 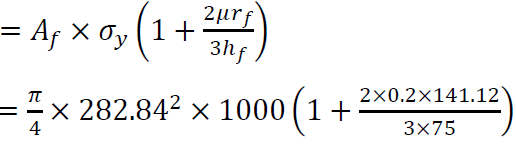
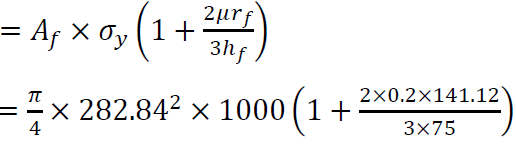
= 78.627 MN

|
Explore Courses for Mechanical Engineering exam
|

|
Question Description
A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer?.
A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer? for Mechanical Engineering 2025 is part of Mechanical Engineering preparation. The Question and answers have been prepared according to the Mechanical Engineering exam syllabus. Information about A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Mechanical Engineering 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer?.
Solutions for A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mechanical Engineering.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Here you can find the meaning of A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A solid cylindrical stainless steel work piece of 200 mm diameter and 150 mm height. This component is reduced by 50% in height with flat die in open die forging. The estimated forging force at the end of the stroke is Assume the flow stress of the material as 1000 MPa and the coefficient of friction to be 0.2a)20.8 kNb)31 MNc)78.6 KNd)78.6 MNCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Mechanical Engineering tests.

|
Explore Courses for Mechanical Engineering exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















