Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > The average number of defects per wafer (defe...
Start Learning for Free
The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?
Correct answer is '0.1847'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
The average number of defects per wafer (defect density) is 3. The red...
Poisson distribution:
A Poisson random variable describes the total number of events that happen in a certain time period.
A discrete random variable X is said to have a Poisson distribution with parameter λ(λ > 0) if the pdf of X is,
Now,
The average number of defects (λ) = 3
For k defects:
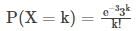
Where X be the number of defects per wafer.
The redundancy will not be sufficient when X > 4
P(X > 4) = 1 − P(X = 0) − P(X = 1) − P(X = 2) − P(X = 3) − P(X = 4)
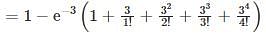
=0.1847
Hence, the correct answer is 0.1847.
Free Test
FREE
| Start Free Test |
Community Answer
The average number of defects per wafer (defect density) is 3. The red...
Defect Density:
The given defect density is 3 defects per wafer. This means that, on average, there are 3 defects per wafer.
Redundancy:
The design allows for up to 4 defects per wafer. This is the maximum number of defects that can be tolerated before the redundancy is considered insufficient.
Poisson Distribution:
The defects are assumed to follow a Poisson distribution. The Poisson distribution is commonly used to model the number of events occurring in a fixed interval of time or space, given the average rate of occurrence.
Calculating the Probability:
To calculate the probability that the redundancy will not be sufficient, we need to find the probability of having more than 4 defects per wafer.
Poisson Probability Formula:
The probability mass function (PMF) of the Poisson distribution is given by the formula:
P(x; λ) = (e^(-λ) * λ^x) / x!
where:
- P(x; λ) is the probability of having x events occur with an average rate of λ.
- e is the base of the natural logarithm (approximately 2.71828).
Calculating the Probability of More than 4 Defects:
To calculate the probability of having more than 4 defects per wafer, we can sum the probabilities of having 5, 6, 7, and so on defects.
P(X > 4) = 1 - P(X <=>
We can use the Poisson PMF formula to calculate the individual probabilities and then sum them up.
P(X > 4) = 1 - [P(0) + P(1) + P(2) + P(3) + P(4)]
Plugging in the average defect density of 3 into the Poisson PMF formula, we get:
P(X > 4) = 1 - [e^(-3) * 3^0 / 0! + e^(-3) * 3^1 / 1! + e^(-3) * 3^2 / 2! + e^(-3) * 3^3 / 3! + e^(-3) * 3^4 / 4!]
Calculating each term and summing them up, we get:
P(X > 4) ≈ 0.1847
Therefore, the probability that the redundancy will not be sufficient is approximately 0.1847 or 18.47%.
The given defect density is 3 defects per wafer. This means that, on average, there are 3 defects per wafer.
Redundancy:
The design allows for up to 4 defects per wafer. This is the maximum number of defects that can be tolerated before the redundancy is considered insufficient.
Poisson Distribution:
The defects are assumed to follow a Poisson distribution. The Poisson distribution is commonly used to model the number of events occurring in a fixed interval of time or space, given the average rate of occurrence.
Calculating the Probability:
To calculate the probability that the redundancy will not be sufficient, we need to find the probability of having more than 4 defects per wafer.
Poisson Probability Formula:
The probability mass function (PMF) of the Poisson distribution is given by the formula:
P(x; λ) = (e^(-λ) * λ^x) / x!
where:
- P(x; λ) is the probability of having x events occur with an average rate of λ.
- e is the base of the natural logarithm (approximately 2.71828).
Calculating the Probability of More than 4 Defects:
To calculate the probability of having more than 4 defects per wafer, we can sum the probabilities of having 5, 6, 7, and so on defects.
P(X > 4) = 1 - P(X <=>
We can use the Poisson PMF formula to calculate the individual probabilities and then sum them up.
P(X > 4) = 1 - [P(0) + P(1) + P(2) + P(3) + P(4)]
Plugging in the average defect density of 3 into the Poisson PMF formula, we get:
P(X > 4) = 1 - [e^(-3) * 3^0 / 0! + e^(-3) * 3^1 / 1! + e^(-3) * 3^2 / 2! + e^(-3) * 3^3 / 3! + e^(-3) * 3^4 / 4!]
Calculating each term and summing them up, we get:
P(X > 4) ≈ 0.1847
Therefore, the probability that the redundancy will not be sufficient is approximately 0.1847 or 18.47%.
Attention Computer Science Engineering (CSE) Students!
To make sure you are not studying endlessly, EduRev has designed Computer Science Engineering (CSE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Computer Science Engineering (CSE).
|
Explore Courses for Computer Science Engineering (CSE) exam
|
|
Similar Computer Science Engineering (CSE) Doubts
Top Courses for Computer Science Engineering (CSE)View all
The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer?
Question Description
The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer?.
The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer?.
Solutions for The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer?, a detailed solution for The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer? has been provided alongside types of The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The average number of defects per wafer (defect density) is 3. The redundancy into the design allows for up to 4 defects per wafer. What is the probability that the redundancy will not be sufficient if the defects follow a Poisson distribution?Correct answer is '0.1847'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.
|
|
Explore Courses for Computer Science Engineering (CSE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup