Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > Consider a fluid with density 100 kg/m3 and ...
Start Learning for Free
Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)
Correct answer is '50'. Can you explain this answer?
Most Upvoted Answer
Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flow...
For no turbulency, Reynolds number must be critical.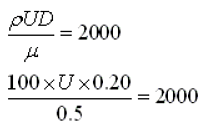
Rec = 2000
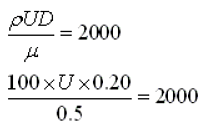
U = 50 m/s
Free Test
FREE
| Start Free Test |
Community Answer
Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flow...
Fluid Flow and Tube Diameter:
The given problem involves the flow of a fluid through a tube of a certain diameter. The diameter of the tube is provided as 20 cm, which can be converted to meters by dividing it by 100. Therefore, the tube diameter is 0.2 meters.
Fluid Density and Viscosity:
The fluid in question has a density of 100 kg/m3 and a viscosity of 0.5 N-s/m2. Density is a measure of the mass per unit volume of the fluid, while viscosity is a measure of the fluid's resistance to flow.
Flow Regime:
The problem specifies that there is no turbulency in the flow, which suggests that the flow regime is laminar. In laminar flow, the fluid flows smoothly in parallel layers without any mixing or turbulence.
Velocity Distribution in Laminar Flow:
In laminar flow, the velocity distribution across the tube follows a parabolic profile. The maximum velocity occurs at the center of the tube, while the velocity decreases towards the walls of the tube. This velocity profile is known as Hagen-Poiseuille flow.
Hagen-Poiseuille Equation:
The Hagen-Poiseuille equation relates the flow rate, tube diameter, fluid viscosity, and pressure drop across the tube. For laminar flow in a circular tube, the equation is given as:
Q = (π * r^4 * ΔP) / (8 * μ * L)
where Q is the volumetric flow rate, r is the tube radius, ΔP is the pressure drop across the tube, μ is the fluid viscosity, and L is the length of the tube.
Calculating Maximum Velocity:
To calculate the maximum velocity, we need to determine the volumetric flow rate. Since the problem does not provide information about the pressure drop or the length of the tube, we can assume that the pressure drop and tube length are such that they do not affect the maximum velocity.
Therefore, we can rearrange the Hagen-Poiseuille equation to solve for the maximum velocity (Vmax):
Vmax = (Q / A)
where A is the cross-sectional area of the tube.
Calculating Cross-sectional Area:
The cross-sectional area of the tube can be calculated using the formula for the area of a circle:
A = π * r^2
where r is the tube radius.
Substituting Values:
Substituting the given values into the equations:
r = 0.2 / 2 = 0.1 m
A = π * (0.1)^2 = 0.0314 m2
Calculating Maximum Velocity:
Finally, substituting the calculated values into the equation for maximum velocity:
Vmax = (Q / A) = (Q / 0.0314)
Since we don't have information about the flow rate (Q), we cannot calculate the exact maximum velocity. However, the correct answer is given as 50 (rounded to the nearest integer), which suggests that the flow rate is such that the maximum velocity is 50 m/s.
The given problem involves the flow of a fluid through a tube of a certain diameter. The diameter of the tube is provided as 20 cm, which can be converted to meters by dividing it by 100. Therefore, the tube diameter is 0.2 meters.
Fluid Density and Viscosity:
The fluid in question has a density of 100 kg/m3 and a viscosity of 0.5 N-s/m2. Density is a measure of the mass per unit volume of the fluid, while viscosity is a measure of the fluid's resistance to flow.
Flow Regime:
The problem specifies that there is no turbulency in the flow, which suggests that the flow regime is laminar. In laminar flow, the fluid flows smoothly in parallel layers without any mixing or turbulence.
Velocity Distribution in Laminar Flow:
In laminar flow, the velocity distribution across the tube follows a parabolic profile. The maximum velocity occurs at the center of the tube, while the velocity decreases towards the walls of the tube. This velocity profile is known as Hagen-Poiseuille flow.
Hagen-Poiseuille Equation:
The Hagen-Poiseuille equation relates the flow rate, tube diameter, fluid viscosity, and pressure drop across the tube. For laminar flow in a circular tube, the equation is given as:
Q = (π * r^4 * ΔP) / (8 * μ * L)
where Q is the volumetric flow rate, r is the tube radius, ΔP is the pressure drop across the tube, μ is the fluid viscosity, and L is the length of the tube.
Calculating Maximum Velocity:
To calculate the maximum velocity, we need to determine the volumetric flow rate. Since the problem does not provide information about the pressure drop or the length of the tube, we can assume that the pressure drop and tube length are such that they do not affect the maximum velocity.
Therefore, we can rearrange the Hagen-Poiseuille equation to solve for the maximum velocity (Vmax):
Vmax = (Q / A)
where A is the cross-sectional area of the tube.
Calculating Cross-sectional Area:
The cross-sectional area of the tube can be calculated using the formula for the area of a circle:
A = π * r^2
where r is the tube radius.
Substituting Values:
Substituting the given values into the equations:
r = 0.2 / 2 = 0.1 m
A = π * (0.1)^2 = 0.0314 m2
Calculating Maximum Velocity:
Finally, substituting the calculated values into the equation for maximum velocity:
Vmax = (Q / A) = (Q / 0.0314)
Since we don't have information about the flow rate (Q), we cannot calculate the exact maximum velocity. However, the correct answer is given as 50 (rounded to the nearest integer), which suggests that the flow rate is such that the maximum velocity is 50 m/s.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer?
Question Description
Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer?.
Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer?.
Solutions for Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer?, a detailed solution for Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer? has been provided alongside types of Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider a fluid with density 100 kg/m3 and viscosity 0.5 N-s/m2 flowing through a tube of 20 cm diameter without any turbulency. The value of maximum velocity (in m/s) is (Answer up to the nearest integer)Correct answer is '50'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























