Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > A flow at a signalised intersection is gover...
Start Learning for Free
A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)
- a)39.9
- b)40.1
Correct answer is between '39.9,40.1'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
A flow at a signalised intersection is governed by the Greenshield mo...
Understanding the Problem
To solve this problem, we need to understand the Greenshield model, which represents the relationship between traffic flow velocity (u) and traffic density (k) at a signalized intersection. The equation of the Greenshield model is given as:
u = 80 - 0.8k
Where u is the velocity in kmph and k is the density in vehicles per km.
The problem states that at a density of 14.65 vehicles per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at maximum flow.
We need to find the magnitude of the speed of the shockwave in kmph.
Solution
To find the magnitude of the speed of the shockwave, we need to determine the change in velocity (Δu) and the change in density (Δk) during the red time period.
Let's calculate Δu and Δk:
Given: k = 14.65 veh/km
Red time = 60 seconds
During the red time period, the flow velocity remains constant at the maximum flow rate. So we can calculate the maximum flow velocity (u_max) using the Greenshield model equation:
u_max = 80 - 0.8k
Substituting the given value of k, we get:
u_max = 80 - 0.8(14.65)
u_max = 80 - 11.72
u_max = 68.28 kmph
The change in velocity (Δu) during the red time period is given by:
Δu = u_max - u
Substituting the maximum flow velocity (u_max) and the velocity at the density of 14.65 veh/km (u), we get:
Δu = 68.28 - (80 - 0.8(14.65))
Δu = 68.28 - (80 - 11.72)
Δu = 68.28 - 68.28
Δu = 0 kmph
During the red time period, there is no change in velocity (Δu = 0 kmph).
Now, let's calculate the change in density (Δk) during the red time period. Since the vehicles move at maximum flow, the density remains constant. Therefore, Δk = 0 veh/km.
The speed of the shockwave is defined as the ratio of the change in velocity (Δu) to the change in density (Δk):
Shockwave speed = Δu / Δk
Substituting the values of Δu and Δk, we get:
Shockwave speed = 0 / 0
The value of 0/0 is undefined. Therefore, the speed of the shockwave cannot be determined directly from the given information.
However, we can make an approximation by considering the initial velocity and density before the red time period. If we assume that the initial velocity is 80 kmph and the initial density is 0 veh/km, we can calculate the shockwave speed as the ratio of the change in velocity (Δu) to the change in density (Δk):
Shockwave speed = Δu / Δk
Substituting the values, we get:
Shockwave speed = (80 -
Free Test
FREE
| Start Free Test |
Community Answer
A flow at a signalised intersection is governed by the Greenshield mo...
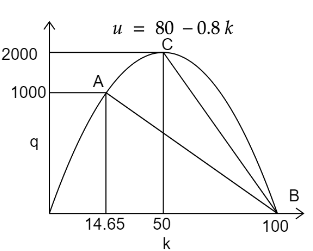
kA = 14.65
u = 80 - 0.8 x 14.65
u = 68.28
qA = 14.65 x 68.28
= 1000 veh/ km
qb = 0
u = 0
Kb = 100
qc = 2000
u = 40
Kc = 50
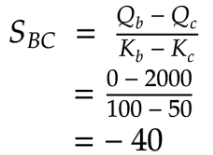
Negative means backward propagation
Attention Civil Engineering (CE) Students!
To make sure you are not studying endlessly, EduRev has designed Civil Engineering (CE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Civil Engineering (CE).
|
Explore Courses for Civil Engineering (CE) exam
|
|
Top Courses for Civil Engineering (CE)View all
A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer?
Question Description
A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer?.
A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer? for Civil Engineering (CE) 2024 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer?.
Solutions for A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer?, a detailed solution for A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer? has been provided alongside types of A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A flow at a signalised intersection is governed by the Greenshield model given by u = 80 - 0.8 k where u is the velocity in kmph and k is the density in veh per km. At the density of 14.65 veh per km, the signal turns red. After a red time of 60 seconds, a shockwave is produced as vehicles move at max flow. The magnitude of the speed of shockwave in kmph will be (round up to nearest integer value)a)39.9b)40.1Correct answer is between '39.9,40.1'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup