Computer Science Engineering (CSE) Exam > Computer Science Engineering (CSE) Questions > Without any additional circuitry, an 8 : 1 MU...
Start Learning for Free
Without any additional circuitry, an 8 : 1 MUX can be used to obtain:
- a)Some but not all functions of 3 variable.
- b)None of the functions of 4 variables.
- c)All functions of the 4 variables.
- d)All functions of 3 variables and some but not all of 4 variables.
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a...
Explanation:
To understand why option 'D' is the correct answer, let's first understand what a multiplexer (MUX) is and how it can be used to obtain different functions.
Multiplexer (MUX):
A multiplexer is a combinational logic circuit that selects one of several input signals and forwards it to a single output line. It has two sets of input lines: one set of data inputs (D0, D1, ..., Dn-1) and another set of control inputs (S0, S1, ..., Sn-1). The control inputs determine which data input is selected and forwarded to the output.
Function of a MUX:
The function of a MUX can be determined by the number of control inputs it has. For an n-bit MUX, it has 2^n input lines and n control inputs. The number of control inputs determines the number of inputs that can be selected.
8 : 1 MUX:
An 8 : 1 MUX has 8 input lines (D0, D1, ..., D7) and 3 control inputs (S0, S1, S2). It selects one of the 8 input lines based on the control inputs and forwards it to the output.
Functions of 3 Variables:
To obtain all functions of 3 variables (A, B, C), we need 2^3 = 8 different functions. Each function can be represented by a truth table with 3 inputs and 1 output.
All functions of 3 variables:
Using an 8 : 1 MUX, we can implement all 8 functions of 3 variables. We can connect each input line (D0, D1, ..., D7) to a specific output based on the truth table of the function we want to implement. The control inputs (S0, S1, S2) can be used to select the appropriate input line.
Functions of 4 Variables:
To obtain all functions of 4 variables (A, B, C, D), we need 2^4 = 16 different functions. Each function can be represented by a truth table with 4 inputs and 1 output.
Some but not all functions of 4 variables:
With an 8 : 1 MUX, we cannot directly implement all 16 functions of 4 variables. This is because there are not enough input lines (8) to represent all the possible combinations of the 4 variables. However, we can still implement some of the functions by using the available input lines and control inputs creatively.
For example, we can implement the functions where the output is solely based on the value of one input variable (A, B, C, or D). In this case, we can connect the input lines corresponding to the selected variable to the output. The remaining input lines can be connected to ground or any other fixed value.
Therefore, an 8 : 1 MUX can be used to obtain all functions of 3 variables and some but not all functions of 4 variables.
To understand why option 'D' is the correct answer, let's first understand what a multiplexer (MUX) is and how it can be used to obtain different functions.
Multiplexer (MUX):
A multiplexer is a combinational logic circuit that selects one of several input signals and forwards it to a single output line. It has two sets of input lines: one set of data inputs (D0, D1, ..., Dn-1) and another set of control inputs (S0, S1, ..., Sn-1). The control inputs determine which data input is selected and forwarded to the output.
Function of a MUX:
The function of a MUX can be determined by the number of control inputs it has. For an n-bit MUX, it has 2^n input lines and n control inputs. The number of control inputs determines the number of inputs that can be selected.
8 : 1 MUX:
An 8 : 1 MUX has 8 input lines (D0, D1, ..., D7) and 3 control inputs (S0, S1, S2). It selects one of the 8 input lines based on the control inputs and forwards it to the output.
Functions of 3 Variables:
To obtain all functions of 3 variables (A, B, C), we need 2^3 = 8 different functions. Each function can be represented by a truth table with 3 inputs and 1 output.
All functions of 3 variables:
Using an 8 : 1 MUX, we can implement all 8 functions of 3 variables. We can connect each input line (D0, D1, ..., D7) to a specific output based on the truth table of the function we want to implement. The control inputs (S0, S1, S2) can be used to select the appropriate input line.
Functions of 4 Variables:
To obtain all functions of 4 variables (A, B, C, D), we need 2^4 = 16 different functions. Each function can be represented by a truth table with 4 inputs and 1 output.
Some but not all functions of 4 variables:
With an 8 : 1 MUX, we cannot directly implement all 16 functions of 4 variables. This is because there are not enough input lines (8) to represent all the possible combinations of the 4 variables. However, we can still implement some of the functions by using the available input lines and control inputs creatively.
For example, we can implement the functions where the output is solely based on the value of one input variable (A, B, C, or D). In this case, we can connect the input lines corresponding to the selected variable to the output. The remaining input lines can be connected to ground or any other fixed value.
Therefore, an 8 : 1 MUX can be used to obtain all functions of 3 variables and some but not all functions of 4 variables.
Free Test
FREE
| Start Free Test |
Community Answer
Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a...
We know that,
A MUX is a combinational circuit that accepts data from multiple input lines and allows the data at the output to pass through a single line.
Select lines decide which input comes at the output.
For an N : 1 MUX
Number of inputs = N
Number of select lines = log2 N
Number of output = 1
A multiplexer with n-data select inputs can implement any function of n-variables and some function of (n + 1) variables.
Example:

Let us consider a 3 variable function.
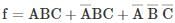
f = Σm(0,3,7)
The function can be implemented by connecting the given minterm to +Vcc and the rest of the minterm to the ground (0 V).
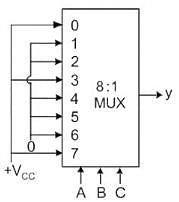
Similarly, any 3 variable functions can be implemented using 8 : 1 MUX.
Let us consider a 4 variable function.

Reducing (1):
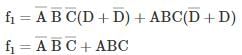
Let us consider another function.


Any 4 variable functions, in which the output does not depend on the 4th variable, can be implemented using 8 : 1 MUX.
f1 can be implemented using 8 : 1 MUX.
f2 cannot be implemented using 8 : 1 MUX.
f2 cannot be implemented using 8 : 1 MUX.
Hence, the correct option is (D).
Attention Computer Science Engineering (CSE) Students!
To make sure you are not studying endlessly, EduRev has designed Computer Science Engineering (CSE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Computer Science Engineering (CSE).

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Similar Computer Science Engineering (CSE) Doubts
Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer?
Question Description
Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer?.
Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer? for Computer Science Engineering (CSE) 2024 is part of Computer Science Engineering (CSE) preparation. The Question and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus. Information about Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer?.
Solutions for Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Computer Science Engineering (CSE).
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Here you can find the meaning of Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer?, a detailed solution for Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Without any additional circuitry, an 8 : 1 MUX can be used to obtain:a)Some but not all functions of 3 variable.b)None of the functions of 4 variables.c)All functions of the 4 variables.d)All functions of 3 variables and some but not all of 4 variables.Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Computer Science Engineering (CSE) tests.

|
Explore Courses for Computer Science Engineering (CSE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























