JEE Exam > JEE Questions > Three points are located at the vertices of ...
Start Learning for Free
Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?
- a)2a/3v
- b)a/v
- c)2a/4v
- d)6a/2v
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Most Upvoted Answer
Three points are located at the vertices of an equilateral triangle w...
Problem: Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?
Solution:
Let the triangle be ABC, with A, B, C denoting the vertices and a being the side length.
Let P, Q, R be the positions of A, B, C respectively at any time t.
At any time t, P is moving towards Q with a velocity of v along the line PQ. Similarly, Q is moving towards R and R is moving towards P.
Let O be the circumcenter of the equilateral triangle ABC.
Since P is moving towards Q, we can draw a line perpendicular to PQ passing through O. Let X be the intersection of this line with PQ.
Similarly, we can draw perpendiculars to QR and RP passing through O, and let Y and Z be the intersections of these perpendiculars with QR and RP respectively.
Then, X, Y, and Z are the midpoints of PQ, QR, and RP respectively, and are also collinear since they lie on the perpendicular bisector of each side of triangle PQR.
Let D be the midpoint of PQ. Then, OD is perpendicular to PQ and OD = a/2 (since O is the circumcenter of ABC).
Similarly, we can define E and F to be the midpoints of QR and RP respectively, such that OE = OF = a/2.
Let T be the intersection of XY and ZF. Then, since XY and ZF are both perpendicular to RP, they are parallel to each other. Therefore, triangle FZT is similar to triangle ODF, with a similarity ratio of 1/2 (since OF = OD = a/2 and FT = DT = a/3).
Therefore, FZ = OD/2 = a/4 and TZ = FZ/2 = a/8.
Since Z is the midpoint of RP, RZ = a/2. Therefore, RT = RZ - TZ = a/2 - a/8 = 3a/8.
Similarly, we can show that QY = a/4 and TP = a/8.
Therefore, the distance between P and R at any time t is PR = PT + TR = a/8 + 3a/8 = a/2.
Therefore, the points P, Q, and R will converge at the center of the equilateral triangle after a time of 2a/3v (since PR = a/2 and the velocity of each point is v).
Solution:
Let the triangle be ABC, with A, B, C denoting the vertices and a being the side length.
Let P, Q, R be the positions of A, B, C respectively at any time t.
At any time t, P is moving towards Q with a velocity of v along the line PQ. Similarly, Q is moving towards R and R is moving towards P.
Let O be the circumcenter of the equilateral triangle ABC.
Since P is moving towards Q, we can draw a line perpendicular to PQ passing through O. Let X be the intersection of this line with PQ.
Similarly, we can draw perpendiculars to QR and RP passing through O, and let Y and Z be the intersections of these perpendiculars with QR and RP respectively.
Then, X, Y, and Z are the midpoints of PQ, QR, and RP respectively, and are also collinear since they lie on the perpendicular bisector of each side of triangle PQR.
Let D be the midpoint of PQ. Then, OD is perpendicular to PQ and OD = a/2 (since O is the circumcenter of ABC).
Similarly, we can define E and F to be the midpoints of QR and RP respectively, such that OE = OF = a/2.
Let T be the intersection of XY and ZF. Then, since XY and ZF are both perpendicular to RP, they are parallel to each other. Therefore, triangle FZT is similar to triangle ODF, with a similarity ratio of 1/2 (since OF = OD = a/2 and FT = DT = a/3).
Therefore, FZ = OD/2 = a/4 and TZ = FZ/2 = a/8.
Since Z is the midpoint of RP, RZ = a/2. Therefore, RT = RZ - TZ = a/2 - a/8 = 3a/8.
Similarly, we can show that QY = a/4 and TP = a/8.
Therefore, the distance between P and R at any time t is PR = PT + TR = a/8 + 3a/8 = a/2.
Therefore, the points P, Q, and R will converge at the center of the equilateral triangle after a time of 2a/3v (since PR = a/2 and the velocity of each point is v).
Free Test
FREE
| Start Free Test |
Community Answer
Three points are located at the vertices of an equilateral triangle w...
Since, the magnitude of velocity remains constant. So, instantaneous tangential acceleration is zero for each particle. So, only centripetal force is present on each particle. The vector sum of forces acting on the particles is zero. So, at every instant the momentum of system remains constant. If the mass of each particle are same. Then the momentum of the system is zero at every instant. So, the centre of mass (centroid) of system remains in rest.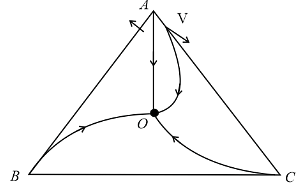
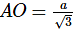
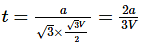
Hence, collision takes place at the centre of mass of system (centroid).
Component of velocity towards O is V cos30

The time of converging = AO / Vcos30
Where
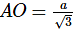
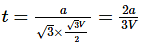
Attention JEE Students!
To make sure you are not studying endlessly, EduRev has designed JEE study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in JEE.

|
Explore Courses for JEE exam
|

|
Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer?
Question Description
Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer?.
Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer? for JEE 2024 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?a)2a/3vb)a/vc)2a/4vd)6a/2vCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.






















