Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Questions > Consider communication over a memoryless bin...
Start Learning for Free
Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).
- a)0.84
- b)0.86
Correct answer is between '0.84,0.86'. Can you explain this answer?
Verified Answer
Consider communication over a memoryless binary symmetric channel usi...
Given that the bits are transmitted using (7, 4) hamming code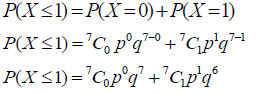
View all questions of this test
∴ Total number of bits n = 7 .
Given that the transmitted bit are received correctly with probability 1- ε .
So, probability of receiving the bits wrongly will be 1-(1 - ε) = ε
Let, p = ε and q = 1 - ε
p = 0.1 and q = 1 - 0.1 = 0.9 (∵ ε = 0.1)
If X is the event of transmitting the bits, then the probability of at most one bit error will be,
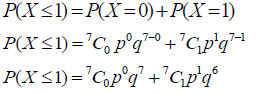
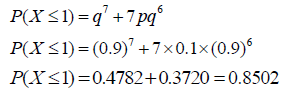
Hence, the correct answer is 0.8502.
Most Upvoted Answer
Consider communication over a memoryless binary symmetric channel usi...
Introduction:
In this problem, we are considering communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. The channel introduces bit errors with a probability of ε and the receiver performs minimum Hamming distance decoding to decode the message bits. We need to calculate the probability that a transmitted codeword is decoded correctly when ε = 0.1.
Hamming Code:
The (7, 4) Hamming code is a linear error-correcting code that adds 3 parity bits to a 4-bit message to create a 7-bit codeword. The parity bits are calculated such that the Hamming distance between any two codewords is at least 3. This allows the receiver to detect and correct single-bit errors.
Probability of Decoding Correctly:
To calculate the probability that a transmitted codeword is decoded correctly, we need to consider the different error patterns that can occur and the corresponding decoding outcomes.
Error Patterns:
1. No errors: The transmitted codeword is received correctly.
2. Single-bit error: One bit in the transmitted codeword is flipped.
3. Double-bit error: Two bits in the transmitted codeword are flipped.
Decoding Outcomes:
1. No errors: The received codeword matches one of the valid codewords. It is correctly decoded.
2. Single-bit error: The received codeword is at a Hamming distance of 1 from one of the valid codewords. It is correctly decoded.
3. Double-bit error: The received codeword is at a Hamming distance of 2 from the valid codewords. It is incorrectly decoded.
Calculation:
To calculate the probability of decoding correctly, we need to sum the probabilities of the decoding outcomes that result in correct decoding.
1. No errors: The probability of no errors is (1-ε)^7.
2. Single-bit error: The probability of a single-bit error is 7ε(1-ε)^6. The factor of 7 represents the 7 possible positions for the error.
3. Double-bit error: The probability of a double-bit error is 7C2 * ε^2 * (1-ε)^5. The factor of 7C2 represents the number of ways to choose 2 positions for the errors.
The probability of decoding correctly is the sum of the probabilities of the first two outcomes:
P(correct) = (1-ε)^7 + 7ε(1-ε)^6
Substituting ε = 0.1, we can calculate the probability:
P(correct) = (0.9)^7 + 7(0.1)(0.9)^6
P(correct) ≈ 0.86
Therefore, the probability that a transmitted codeword is decoded correctly when ε = 0.1 is approximately 0.86.
In this problem, we are considering communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. The channel introduces bit errors with a probability of ε and the receiver performs minimum Hamming distance decoding to decode the message bits. We need to calculate the probability that a transmitted codeword is decoded correctly when ε = 0.1.
Hamming Code:
The (7, 4) Hamming code is a linear error-correcting code that adds 3 parity bits to a 4-bit message to create a 7-bit codeword. The parity bits are calculated such that the Hamming distance between any two codewords is at least 3. This allows the receiver to detect and correct single-bit errors.
Probability of Decoding Correctly:
To calculate the probability that a transmitted codeword is decoded correctly, we need to consider the different error patterns that can occur and the corresponding decoding outcomes.
Error Patterns:
1. No errors: The transmitted codeword is received correctly.
2. Single-bit error: One bit in the transmitted codeword is flipped.
3. Double-bit error: Two bits in the transmitted codeword are flipped.
Decoding Outcomes:
1. No errors: The received codeword matches one of the valid codewords. It is correctly decoded.
2. Single-bit error: The received codeword is at a Hamming distance of 1 from one of the valid codewords. It is correctly decoded.
3. Double-bit error: The received codeword is at a Hamming distance of 2 from the valid codewords. It is incorrectly decoded.
Calculation:
To calculate the probability of decoding correctly, we need to sum the probabilities of the decoding outcomes that result in correct decoding.
1. No errors: The probability of no errors is (1-ε)^7.
2. Single-bit error: The probability of a single-bit error is 7ε(1-ε)^6. The factor of 7 represents the 7 possible positions for the error.
3. Double-bit error: The probability of a double-bit error is 7C2 * ε^2 * (1-ε)^5. The factor of 7C2 represents the number of ways to choose 2 positions for the errors.
The probability of decoding correctly is the sum of the probabilities of the first two outcomes:
P(correct) = (1-ε)^7 + 7ε(1-ε)^6
Substituting ε = 0.1, we can calculate the probability:
P(correct) = (0.9)^7 + 7(0.1)(0.9)^6
P(correct) ≈ 0.86
Therefore, the probability that a transmitted codeword is decoded correctly when ε = 0.1 is approximately 0.86.
Free Test
FREE
| Start Free Test |
Community Answer
Consider communication over a memoryless binary symmetric channel usi...
Given that the bits are transmitted using (7, 4) hamming code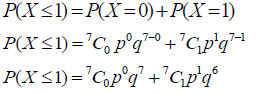
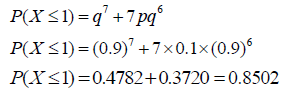
∴ Total number of bits n = 7 .
Given that the transmitted bit are received correctly with probability 1- ε .
So, probability of receiving the bits wrongly will be 1-(1 - ε) = ε
Let, p = ε and q = 1 - ε
p = 0.1 and q = 1 - 0.1 = 0.9 (∵ ε = 0.1)
If X is the event of transmitting the bits, then the probability of at most one bit error will be,
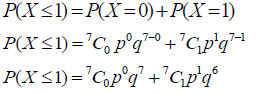
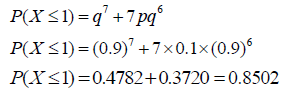
Hence, the correct answer is 0.8502.

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Similar Electronics and Communication Engineering (ECE) Doubts
Question Description
Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2025 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer?.
Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2025 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer?.
Solutions for Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electronics and Communication Engineering (ECE).
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Here you can find the meaning of Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer?, a detailed solution for Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer? has been provided alongside types of Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider communication over a memoryless binary symmetric channel using a (7, 4) Hamming code. Each transmitted bit is received correctly with probability (1 - ε) , and flipped with probability ε . For each codeword transmission, the receiver performs minimum Hamming distance decoding, and correctly decodes the message bits if and only if the channel introduces at most one bit error. For ε = 0.1, the probability that a transmitted codeword is decoded correctly is _________ (round off to two decimal places).a)0.84b)0.86Correct answer is between '0.84,0.86'. Can you explain this answer? tests, examples and also practice Electronics and Communication Engineering (ECE) tests.

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























