Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > Which of the following is the correct relatio...
Start Learning for Free
Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?
- a)G is always below P
- b)P is always below G
- c)G is either at P or below it.
- d)P is either at G or below it.
Correct answer is option 'D'. Can you explain this answer?
Most Upvoted Answer
Which of the following is the correct relation between centroid (G) an...
Relation between Centroid and Centre of Pressure of a Plane Submerged in a Liquid
The centroid (G) is the point at which the entire weight of the submerged plane can be assumed to act upon. The centre of pressure (P) is the point at which the resultant pressure force can be assumed to act upon.
Determination of Centroid and Centre of Pressure
The centroid of the submerged plane can be determined by using the principle of moments. The plane is divided into small strips, and the moment of each strip about a reference point is calculated. The centroid is the point at which the sum of these moments is zero.
The centre of pressure can be determined by using the principle of moments as well. The plane is again divided into small strips, and the pressure force acting on each strip is calculated. The centre of pressure is the point at which the sum of the moments of these pressure forces is zero.
Relation between Centroid and Centre of Pressure
The relation between the centroid and centre of pressure depends on the shape of the submerged plane. In general, the following relations hold true:
- If the plane is symmetrical about its vertical axis, the centroid and centre of pressure coincide.
- If the plane is not symmetrical about its vertical axis, the centroid and centre of pressure are not in the same location. In this case, the centre of pressure is always below the centroid.
- If the plane is inclined, the centre of pressure moves towards the lower end of the plane.
Conclusion
In conclusion, the correct relation between the centroid and centre of pressure of a plane submerged in a liquid is that the centre of pressure is either at the centroid or below it. The exact location of the centre of pressure depends on the shape and orientation of the submerged plane.
The centroid (G) is the point at which the entire weight of the submerged plane can be assumed to act upon. The centre of pressure (P) is the point at which the resultant pressure force can be assumed to act upon.
Determination of Centroid and Centre of Pressure
The centroid of the submerged plane can be determined by using the principle of moments. The plane is divided into small strips, and the moment of each strip about a reference point is calculated. The centroid is the point at which the sum of these moments is zero.
The centre of pressure can be determined by using the principle of moments as well. The plane is again divided into small strips, and the pressure force acting on each strip is calculated. The centre of pressure is the point at which the sum of the moments of these pressure forces is zero.
Relation between Centroid and Centre of Pressure
The relation between the centroid and centre of pressure depends on the shape of the submerged plane. In general, the following relations hold true:
- If the plane is symmetrical about its vertical axis, the centroid and centre of pressure coincide.
- If the plane is not symmetrical about its vertical axis, the centroid and centre of pressure are not in the same location. In this case, the centre of pressure is always below the centroid.
- If the plane is inclined, the centre of pressure moves towards the lower end of the plane.
Conclusion
In conclusion, the correct relation between the centroid and centre of pressure of a plane submerged in a liquid is that the centre of pressure is either at the centroid or below it. The exact location of the centre of pressure depends on the shape and orientation of the submerged plane.
Free Test
FREE
| Start Free Test |
Community Answer
Which of the following is the correct relation between centroid (G) an...
The depth of the centroid 
and the centre of pressure yCP are related by:
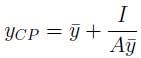
where I = the moment of inertia and A= area. None of the quantities I, A and
can be negative. Thus, YCP >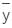 
. For horizontal planes, I = 0, hence YCP =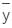 
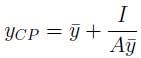
and the centre of pressure yCP are related by:where I = the moment of inertia and A= area. None of the quantities I, A and
can be negative. Thus, YCP > 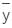. For horizontal planes, I = 0, hence YCP =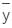
|
Explore Courses for Civil Engineering (CE) exam
|
|
Top Courses for Civil Engineering (CE)View all
Question Description
Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer?.
Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer?.
Solutions for Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer?, a detailed solution for Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following is the correct relation between centroid (G) and the centre of pressure (P) of a plane submerged in a liquid?a)G is always below Pb)P is always below Gc)G is either at P or below it.d)P is either at G or below it.Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup