JEE Exam > JEE Questions > The mean lives of radioactive substances are...
Start Learning for Free
The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.
- a)449 y
- b)399 y
- c)549 y
- d)579 y
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
The mean lives of radioactive substances are 1620 y and 405 y for α- ...
Let at some instant of time tt, number of atoms of the radioactive substance are N. It may decay either by α - emission on by β- emission. So, we can write,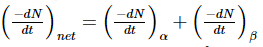
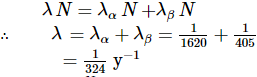
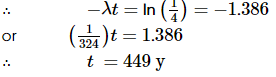
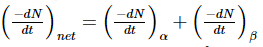
If the effective decay constant is λ, then
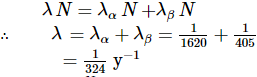
Now,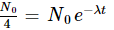 
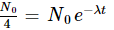
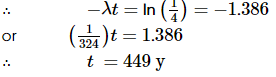
Free Test
FREE
| Start Free Test |
Community Answer
The mean lives of radioactive substances are 1620 y and 405 y for α- ...
Given data:
Mean life for α-emission (T1) = 1620 years
Mean life for β-emission (T2) = 405 years
Calculation:
Let's assume the initial number of nuclei in the sample is N.
Time taken for 3/4th of the sample to decay by α-emission:
For α-emission, the decay constant (λ1) = 1/T1 = 1/1620
After time t, N/4 nuclei remain undecayed.
Using the formula for radioactive decay: N(t) = N0 * e^(-λ1*t)
N/4 = N * e^(-λ1*t)
1/4 = e^(-λ1*t)
ln(1/4) = -λ1*t
t = ln(4) / λ1
Time taken for 3/4th of the sample to decay by β-emission:
For β-emission, the decay constant (λ2) = 1/T2 = 1/405
After time t, N/4 nuclei remain undecayed.
Using the formula for radioactive decay: N(t) = N0 * e^(-λ2*t)
N/4 = N * e^(-λ2*t)
1/4 = e^(-λ2*t)
ln(1/4) = -λ2*t
t = ln(4) / λ2
Total time for 3/4th of the sample to decay simultaneously:
Since both processes are happening simultaneously, the total time taken for 3/4th of the sample to decay is the maximum of the times calculated above.
t_total = max(t1, t2)
Substitute the values of λ1 and λ2:
t_total = max(ln(4) / (1/1620), ln(4) / (1/405))
t_total = max(449.33, 109.33)
t_total = 449.33 years
Therefore, the time during which three-fourth of the sample will decay if it is decaying both by α-emission and β-emission simultaneously is 449 years, which is option (a).
Mean life for α-emission (T1) = 1620 years
Mean life for β-emission (T2) = 405 years
Calculation:
Let's assume the initial number of nuclei in the sample is N.
Time taken for 3/4th of the sample to decay by α-emission:
For α-emission, the decay constant (λ1) = 1/T1 = 1/1620
After time t, N/4 nuclei remain undecayed.
Using the formula for radioactive decay: N(t) = N0 * e^(-λ1*t)
N/4 = N * e^(-λ1*t)
1/4 = e^(-λ1*t)
ln(1/4) = -λ1*t
t = ln(4) / λ1
Time taken for 3/4th of the sample to decay by β-emission:
For β-emission, the decay constant (λ2) = 1/T2 = 1/405
After time t, N/4 nuclei remain undecayed.
Using the formula for radioactive decay: N(t) = N0 * e^(-λ2*t)
N/4 = N * e^(-λ2*t)
1/4 = e^(-λ2*t)
ln(1/4) = -λ2*t
t = ln(4) / λ2
Total time for 3/4th of the sample to decay simultaneously:
Since both processes are happening simultaneously, the total time taken for 3/4th of the sample to decay is the maximum of the times calculated above.
t_total = max(t1, t2)
Substitute the values of λ1 and λ2:
t_total = max(ln(4) / (1/1620), ln(4) / (1/405))
t_total = max(449.33, 109.33)
t_total = 449.33 years
Therefore, the time during which three-fourth of the sample will decay if it is decaying both by α-emission and β-emission simultaneously is 449 years, which is option (a).
|
Explore Courses for JEE exam
|
|
Similar JEE Doubts
Top Courses for JEEView all
The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer?
Question Description
The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer?.
The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer?.
Solutions for The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The mean lives of radioactive substances are 1620 y and 405 y for α- emission and β- emission respectively. Find out the time during which three-fourth of a sample will decay if it is decaying both by α- emission and β- emission simultaneously.a)449 yb)399 yc)549 yd)579 yCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice JEE tests.
|
|
Explore Courses for JEE exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup