Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > When a cantilever beam is loaded at its free ...
Start Learning for Free
When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop at
- a)bottom fibre
- b)top fibre
- c)neutral axis
- d)centre of gravity
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
When a cantilever beam is loaded at its free end, the maximum compress...
Introduction:
When a cantilever beam is loaded at its free end, it experiences various internal stresses due to the applied load. These stresses are distributed across the cross-section of the beam. The maximum compressive stress, also known as the principal stress, is an important parameter to determine the beam's strength and stability.
Explanation:
The maximum compressive stress in a cantilever beam loaded at its free end develops at the bottom fiber of the beam. This can be understood by considering the behavior of the beam under loading.
1. Bending Stress Distribution:
When a cantilever beam is subjected to a load at its free end, it undergoes bending deformation. The top fibers of the beam experience tensile stresses, while the bottom fibers experience compressive stresses.
2. Neutral Axis:
The neutral axis is an imaginary line within the beam cross-section that experiences no stress during bending. It lies at the centroid of the cross-section and divides the beam into top and bottom fibers.
3. Maximum Compressive Stress:
The maximum compressive stress occurs at the bottom fiber of the beam. This is because the bottom fibers are located farthest away from the neutral axis and experience the highest compressive forces during bending.
4. Stress Distribution:
As we move away from the neutral axis towards the bottom fiber, the compressive stress increases. At the bottom fiber, the stress reaches its maximum value. Conversely, as we move away from the neutral axis towards the top fiber, the stress decreases until it becomes zero at the neutral axis.
5. Importance of Maximum Compressive Stress:
The maximum compressive stress is crucial in determining the beam's strength and stability. If the compressive stress exceeds the material's compressive strength, it may lead to failure, such as buckling or crushing of the beam.
Conclusion:
In a cantilever beam loaded at its free end, the maximum compressive stress develops at the bottom fiber of the beam. This occurs due to the bending deformation and stress distribution across the beam's cross-section. Understanding the distribution of stresses is essential for designing beams that can withstand the applied loads without failure.
When a cantilever beam is loaded at its free end, it experiences various internal stresses due to the applied load. These stresses are distributed across the cross-section of the beam. The maximum compressive stress, also known as the principal stress, is an important parameter to determine the beam's strength and stability.
Explanation:
The maximum compressive stress in a cantilever beam loaded at its free end develops at the bottom fiber of the beam. This can be understood by considering the behavior of the beam under loading.
1. Bending Stress Distribution:
When a cantilever beam is subjected to a load at its free end, it undergoes bending deformation. The top fibers of the beam experience tensile stresses, while the bottom fibers experience compressive stresses.
2. Neutral Axis:
The neutral axis is an imaginary line within the beam cross-section that experiences no stress during bending. It lies at the centroid of the cross-section and divides the beam into top and bottom fibers.
3. Maximum Compressive Stress:
The maximum compressive stress occurs at the bottom fiber of the beam. This is because the bottom fibers are located farthest away from the neutral axis and experience the highest compressive forces during bending.
4. Stress Distribution:
As we move away from the neutral axis towards the bottom fiber, the compressive stress increases. At the bottom fiber, the stress reaches its maximum value. Conversely, as we move away from the neutral axis towards the top fiber, the stress decreases until it becomes zero at the neutral axis.
5. Importance of Maximum Compressive Stress:
The maximum compressive stress is crucial in determining the beam's strength and stability. If the compressive stress exceeds the material's compressive strength, it may lead to failure, such as buckling or crushing of the beam.
Conclusion:
In a cantilever beam loaded at its free end, the maximum compressive stress develops at the bottom fiber of the beam. This occurs due to the bending deformation and stress distribution across the beam's cross-section. Understanding the distribution of stresses is essential for designing beams that can withstand the applied loads without failure.
Free Test
FREE
| Start Free Test |
Community Answer
When a cantilever beam is loaded at its free end, the maximum compress...
Reinforced Concrete Structures Question 5 Detailed Solution
Concept:
When a cantilever beam is loaded vertically downward, then all the fibers above the neutral axis got elongated and all the fibers below the neutral axis got contracted due to which tensile stress is induced in all fibers above the neutral axis and compressive stress is induced in all fibers below the neutral axis.
Therefore, the maximum compressive stress will be at the bottom fiber, because that fiber has minimum section modulus.
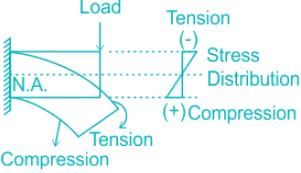
Concept:
When a cantilever beam is loaded vertically downward, then all the fibers above the neutral axis got elongated and all the fibers below the neutral axis got contracted due to which tensile stress is induced in all fibers above the neutral axis and compressive stress is induced in all fibers below the neutral axis.
Therefore, the maximum compressive stress will be at the bottom fiber, because that fiber has minimum section modulus.


|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer?.
When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer?.
Solutions for When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice When a cantilever beam is loaded at its free end, the maximum compressive stress shall develop ata)bottom fibreb)top fibrec)neutral axisd)centre of gravityCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























