Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > What is the condition for critical flow?a)Q/g...
Start Learning for Free
What is the condition for critical flow?
- a)Q/g = A/T
- b)Q2/g = A2/T
- c)Q/g = A3/T
- d)Q2/g = A3/T
Correct answer is option 'D'. Can you explain this answer?
Most Upvoted Answer
What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g ...
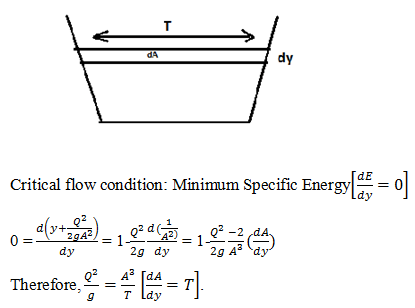
Free Test
FREE
| Start Free Test |
Community Answer
What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g ...
The condition for critical flow in open channel hydraulics is given by the equation Q^2/g = A^3/T, where Q is the flow rate, g is the acceleration due to gravity, A is the cross-sectional area of flow, and T is the top width of the flow.
Explanation:
The condition for critical flow is based on the principle of conservation of energy. When a fluid flows through an open channel, it possesses kinetic energy due to its velocity and potential energy due to its elevation. In critical flow, the flow velocity is the maximum possible for a given flow rate, resulting in the minimum specific energy.
Here is a detailed explanation of each term in the equation:
1. Q (Flow Rate): It represents the volume of fluid passing through a given cross-section per unit time. It is measured in cubic meters per second (m^3/s).
2. g (Acceleration due to Gravity): It is a constant value that represents the rate at which objects accelerate towards the Earth. The standard value for gravity is approximately 9.81 m/s^2.
3. A (Cross-sectional Area of Flow): It refers to the area of the channel cross-section perpendicular to the flow direction. It is measured in square meters (m^2). In critical flow, the cross-sectional area is directly related to the flow rate.
4. T (Top Width of Flow): It represents the width of the flow at the water surface. It is measured in meters (m). In critical flow, the top width is inversely related to the flow rate.
The equation Q^2/g = A^3/T is derived from the energy equation for open channel flow. It states that the square of the flow rate divided by the acceleration due to gravity is equal to the cube of the cross-sectional area divided by the top width of the flow. This equation is satisfied when the flow is in a critical state.
In critical flow, the flow velocity is equal to the critical velocity, which is the speed at which the specific energy of the flow is minimum. Any increase or decrease in flow rate will result in a transition from subcritical to supercritical or vice versa. Critical flow is important in various hydraulic calculations, such as determining the design of channels, culverts, and spillways.
To summarize, the condition for critical flow in open channel hydraulics is given by the equation Q^2/g = A^3/T. This equation relates the flow rate, cross-sectional area, top width, and acceleration due to gravity to determine the critical flow conditions.
Explanation:
The condition for critical flow is based on the principle of conservation of energy. When a fluid flows through an open channel, it possesses kinetic energy due to its velocity and potential energy due to its elevation. In critical flow, the flow velocity is the maximum possible for a given flow rate, resulting in the minimum specific energy.
Here is a detailed explanation of each term in the equation:
1. Q (Flow Rate): It represents the volume of fluid passing through a given cross-section per unit time. It is measured in cubic meters per second (m^3/s).
2. g (Acceleration due to Gravity): It is a constant value that represents the rate at which objects accelerate towards the Earth. The standard value for gravity is approximately 9.81 m/s^2.
3. A (Cross-sectional Area of Flow): It refers to the area of the channel cross-section perpendicular to the flow direction. It is measured in square meters (m^2). In critical flow, the cross-sectional area is directly related to the flow rate.
4. T (Top Width of Flow): It represents the width of the flow at the water surface. It is measured in meters (m). In critical flow, the top width is inversely related to the flow rate.
The equation Q^2/g = A^3/T is derived from the energy equation for open channel flow. It states that the square of the flow rate divided by the acceleration due to gravity is equal to the cube of the cross-sectional area divided by the top width of the flow. This equation is satisfied when the flow is in a critical state.
In critical flow, the flow velocity is equal to the critical velocity, which is the speed at which the specific energy of the flow is minimum. Any increase or decrease in flow rate will result in a transition from subcritical to supercritical or vice versa. Critical flow is important in various hydraulic calculations, such as determining the design of channels, culverts, and spillways.
To summarize, the condition for critical flow in open channel hydraulics is given by the equation Q^2/g = A^3/T. This equation relates the flow rate, cross-sectional area, top width, and acceleration due to gravity to determine the critical flow conditions.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer?.
What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer?.
Solutions for What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice What is the condition for critical flow?a)Q/g = A/Tb)Q2/g = A2/Tc)Q/g = A3/Td)Q2/g = A3/TCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















