Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > The chainages (m) and corresponding perpendic...
Start Learning for Free
The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpson's rule is
- a)681
- b)767.825
- c)781
- d)790.5
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
The chainages (m) and corresponding perpendicular offsets(m) taken fro...
Given data:
Chainages (m) and corresponding perpendicular offsets (m) taken from a chain line to an irregular boundary are as follows:
(0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00), and (210, 5.80)
To find:
The area (m²) between the chain line and the irregular boundary using Simpson's rule.
Explanation:
Simpson's rule is a numerical integration method used to approximate the area under a curve. It provides a better approximation compared to other methods like the trapezoidal rule when the curve is not linear.
The formula for Simpson's rule is:
Area = (h/3) * [y0 + 4y1 + 2y2 + 4y3 + 2y4 + ... + 2yn-2 + 4yn-1 + yn]
Where:
h = step size (difference between consecutive chainages)
y0, y1, y2, ..., yn = perpendicular offsets at respective chainages
Step 1: Calculate the step size (h)
h = (210 - 0) / (n-1)
= 210 / (8-1)
= 210 / 7
= 30
Step 2: Calculate the sum of perpendicular offsets based on the given data:
Sum of even offsets = y2 + y4 + y6
= 3.80 + 4.65 + 5.00
= 13.45
Sum of odd offsets = y1 + y3 + y5 + y7
= 2.65 + 3.75 + 3.60 + 5.80
= 15.80
Step 3: Calculate the area using Simpson's rule:
Area = (h/3) * [y0 + 4y1 + 2y2 + 4y3 + 2y4 + 4y5 + 2y6 + 4y7 + yn]
= (30/3) * [0 + 4(2.65) + 2(3.80) + 4(3.75) + 2(4.65) + 4(3.60) + 2(5.00) + 4(5.80) + 0]
= 10 * [0 + 10.60 + 7.60 + 15.00 + 9.30 + 14.40 + 10.00 + 23.20 + 0]
= 10 * 90.10
= 901
Step 4: Calculate the adjusted area by multiplying by the step size (h/2):
Adjusted area = Area * (h/2)
= 901 * (30/2)
= 901 * 15
= 13515
Step 5: Round the final result to the nearest whole number:
Final area = 13515 (rounded to the nearest whole number)
=
Chainages (m) and corresponding perpendicular offsets (m) taken from a chain line to an irregular boundary are as follows:
(0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00), and (210, 5.80)
To find:
The area (m²) between the chain line and the irregular boundary using Simpson's rule.
Explanation:
Simpson's rule is a numerical integration method used to approximate the area under a curve. It provides a better approximation compared to other methods like the trapezoidal rule when the curve is not linear.
The formula for Simpson's rule is:
Area = (h/3) * [y0 + 4y1 + 2y2 + 4y3 + 2y4 + ... + 2yn-2 + 4yn-1 + yn]
Where:
h = step size (difference between consecutive chainages)
y0, y1, y2, ..., yn = perpendicular offsets at respective chainages
Step 1: Calculate the step size (h)
h = (210 - 0) / (n-1)
= 210 / (8-1)
= 210 / 7
= 30
Step 2: Calculate the sum of perpendicular offsets based on the given data:
Sum of even offsets = y2 + y4 + y6
= 3.80 + 4.65 + 5.00
= 13.45
Sum of odd offsets = y1 + y3 + y5 + y7
= 2.65 + 3.75 + 3.60 + 5.80
= 15.80
Step 3: Calculate the area using Simpson's rule:
Area = (h/3) * [y0 + 4y1 + 2y2 + 4y3 + 2y4 + 4y5 + 2y6 + 4y7 + yn]
= (30/3) * [0 + 4(2.65) + 2(3.80) + 4(3.75) + 2(4.65) + 4(3.60) + 2(5.00) + 4(5.80) + 0]
= 10 * [0 + 10.60 + 7.60 + 15.00 + 9.30 + 14.40 + 10.00 + 23.20 + 0]
= 10 * 90.10
= 901
Step 4: Calculate the adjusted area by multiplying by the step size (h/2):
Adjusted area = Area * (h/2)
= 901 * (30/2)
= 901 * 15
= 13515
Step 5: Round the final result to the nearest whole number:
Final area = 13515 (rounded to the nearest whole number)
=
Free Test
FREE
| Start Free Test |
Community Answer
The chainages (m) and corresponding perpendicular offsets(m) taken fro...
Simpson's Rule:
In this rule, the boundaries between the ends of ordinates are assumed to form an arc of a parabola. Hence, Simpson's rule is sometimes called the parabolic rule.
The rule may be stated as follows,
To the sum of the first and the last ordinate, four times the sum of even ordinates and twice the sum of the remaining odd ordinates are added. This total sum is multiplied by the common distance. One-third of this product is the required area.
The area is given by Simpson's rule:

where O1, O2, O3, .........On is the offset
Limitation:
This rule is applicable only when the number of divisions is even, i.e., the number of ordinates is odd.
Calculation
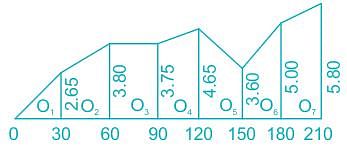
Simpson's Rule :- If this rule is to be applied, the number of ordinates must be odd. But here the number of ordinate is even (eight)
so, Simpson's rule is applied from 01 to 07 and the area between 07 and 08 is found out by trapezoidal rule.
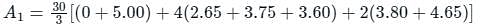
A1 = 10 × (5 + 40 + 16.9)
A1 = 619 m2
A2 = 30/2(5.00+5.80)
A2 = 162 m2
∴ Total area = A1 + A2
= 619 + 162 = 781 m2
In this rule, the boundaries between the ends of ordinates are assumed to form an arc of a parabola. Hence, Simpson's rule is sometimes called the parabolic rule.
The rule may be stated as follows,
To the sum of the first and the last ordinate, four times the sum of even ordinates and twice the sum of the remaining odd ordinates are added. This total sum is multiplied by the common distance. One-third of this product is the required area.
The area is given by Simpson's rule:

where O1, O2, O3, .........On is the offset
Limitation:
This rule is applicable only when the number of divisions is even, i.e., the number of ordinates is odd.
Calculation

Simpson's Rule :- If this rule is to be applied, the number of ordinates must be odd. But here the number of ordinate is even (eight)
so, Simpson's rule is applied from 01 to 07 and the area between 07 and 08 is found out by trapezoidal rule.
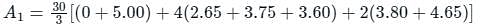
A1 = 10 × (5 + 40 + 16.9)
A1 = 619 m2
A2 = 30/2(5.00+5.80)
A2 = 162 m2
∴ Total area = A1 + A2
= 619 + 162 = 781 m2

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer?
Question Description
The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer?.
The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer?.
Solutions for The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer?, a detailed solution for The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The chainages (m) and corresponding perpendicular offsets(m) taken from a chain line to an irregular boundary were (0, 0), (30, 2.65), (60, 3.80), (90, 3.75), (120, 4.65), (150, 3.60), (180, 5.00) and (210, 5.80). The area (m2) between the chain line and the irregular boundary by Simpsons rule isa)681b)767.825c)781d)790.5Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























