Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > Prismoidal correction, while surveying is alw...
Start Learning for Free
Prismoidal correction, while surveying is always?
- a)Exponentially subtractive
- b)Exponentially additive
- c)Subtractive
- d)Additive
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
Prismoidal correction, while surveying is always?a)Exponentially subtr...
Prismoidal correction in surveying
Prismoidal correction is a term used in surveying to account for the errors that occur when calculating the volume of a prismoidal-shaped object. A prismoid is a three-dimensional geometric shape that has two parallel bases and four lateral faces that are trapezoids.
Prismoidal correction is necessary because when calculating the volume of a prismoid using the formula V = (A1 + A2 + √(A1 * A2))/3 * h, where A1 and A2 are the areas of the bases and h is the height, there is a discrepancy between the calculated volume and the actual volume. This discrepancy arises because the formula assumes the prismoid to be a perfect geometric shape, which is rarely the case in real-world surveying.
Subtractive correction
When applying prismoidal correction, we need to consider whether the correction should be subtractive or additive. The correct answer to the given question is option 'c', which states that the correction is subtractive. Let's understand why prismoidal correction is subtractive.
When the surveyed prismoid is compared to a perfect geometric shape, it is common for the actual volume to be less than the calculated volume. This is because the trapezoidal faces of the prismoid are not perfectly flat and straight, which leads to a smaller volume. Therefore, to correct for this discrepancy, we subtract a certain value from the calculated volume.
The subtractive correction compensates for the excess volume that is obtained by assuming a perfect geometric shape. By subtracting a value from the calculated volume, we can obtain a more accurate representation of the actual volume of the prismoid.
Conclusion
In conclusion, prismoidal correction in surveying is subtractive in nature. This correction is necessary because the calculated volume of a prismoid using a perfect geometric shape does not accurately represent the actual volume due to the real-world imperfections of the shape. Subtracting a correction value allows for a more accurate estimation of the volume of the prismoid.
Prismoidal correction is a term used in surveying to account for the errors that occur when calculating the volume of a prismoidal-shaped object. A prismoid is a three-dimensional geometric shape that has two parallel bases and four lateral faces that are trapezoids.
Prismoidal correction is necessary because when calculating the volume of a prismoid using the formula V = (A1 + A2 + √(A1 * A2))/3 * h, where A1 and A2 are the areas of the bases and h is the height, there is a discrepancy between the calculated volume and the actual volume. This discrepancy arises because the formula assumes the prismoid to be a perfect geometric shape, which is rarely the case in real-world surveying.
Subtractive correction
When applying prismoidal correction, we need to consider whether the correction should be subtractive or additive. The correct answer to the given question is option 'c', which states that the correction is subtractive. Let's understand why prismoidal correction is subtractive.
When the surveyed prismoid is compared to a perfect geometric shape, it is common for the actual volume to be less than the calculated volume. This is because the trapezoidal faces of the prismoid are not perfectly flat and straight, which leads to a smaller volume. Therefore, to correct for this discrepancy, we subtract a certain value from the calculated volume.
The subtractive correction compensates for the excess volume that is obtained by assuming a perfect geometric shape. By subtracting a value from the calculated volume, we can obtain a more accurate representation of the actual volume of the prismoid.
Conclusion
In conclusion, prismoidal correction in surveying is subtractive in nature. This correction is necessary because the calculated volume of a prismoid using a perfect geometric shape does not accurately represent the actual volume due to the real-world imperfections of the shape. Subtracting a correction value allows for a more accurate estimation of the volume of the prismoid.
Free Test
FREE
| Start Free Test |
Community Answer
Prismoidal correction, while surveying is always?a)Exponentially subtr...
The volume of earthwork by trapezoidal method = V1

The volume of earthwork by prismoidal formula = V2

Prismoidal correction

The volume of earthwork by prismoidal formula = V2

Prismoidal correction
- The volume by the prismoidal formula is more accurate than any other method
- But the trapezoidal method is more often used for calculating the volume of earthwork in the field.
- The difference between the volume computed by the trapezoidal formula and the prismoidal formula is known as a prismoidal correction.
- Since the trapezoidal formula always overestimates the volume, the prismoidal correction is always subtractive in nature is usually more than calculated by the prismoidal formula, therefore the prismoidal correction is generally subtractive.
- Volume by prismoidal formula = volume by the trapezoidal formula - prismoidal correction
Prismoidal correction (CP)
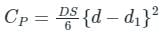
Where, D = Distance between the sections, S (Horizontal) : 1 (Vertical) = Side slope, d and d1 are the depth of earthwork at the centerline
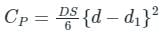
Where, D = Distance between the sections, S (Horizontal) : 1 (Vertical) = Side slope, d and d1 are the depth of earthwork at the centerline

|
Explore Courses for Civil Engineering (CE) exam
|

|
Similar Civil Engineering (CE) Doubts
Question Description
Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer?.
Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Prismoidal correction, while surveying is always?a)Exponentially subtractiveb)Exponentially additivec)Subtractived)AdditiveCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























