Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Questions > If the range of a radar is to be doubled, the...
Start Learning for Free
If the range of a radar is to be doubled, the peak transmit power of the radar has to be
- a)increased by a factor of 2
- b)increased by a factor of 4
- c)decreased by a factor of 4
- d)increased by a factor of 16
Correct answer is option 'D'. Can you explain this answer?
Most Upvoted Answer
If the range of a radar is to be doubled, the peak transmit power of t...
Explanation:
To understand why the peak transmit power of the radar has to be increased by a factor of 16 when the range is doubled, we need to consider the basic principles of radar operation.
Radar Operation:
Radar works by transmitting a high-frequency electromagnetic wave, known as a radar pulse, and then detecting the echo reflected back from a target. The time taken for the pulse to travel to the target and return is used to calculate the range or distance to the target.
Radar Range Equation:
The range or distance to a target can be calculated using the radar range equation:
R = (c * Δt) / 2
Where:
R = Range to the target
c = Speed of light
Δt = Time taken for the pulse to travel to the target and return
Relationship between Transmit Power and Range:
In the radar range equation, the time taken for the pulse to travel to the target and return (Δt) is directly proportional to the range (R). This means that to increase the range, the time taken for the pulse to travel to the target and return must be increased.
The time taken for the pulse to travel to the target and return is determined by the speed of light (c) and the distance traveled by the pulse. Since the speed of light is constant, the distance traveled by the pulse needs to be increased to increase the time taken.
To increase the distance traveled by the pulse, the transmit power of the radar needs to be increased. This is because the power of the radar pulse decreases with distance due to spreading and attenuation effects.
Relationship between Transmit Power and Range:
The power of a radar pulse decreases with distance according to the inverse square law:
P = P0 / (4πR²)
Where:
P = Power of the radar pulse at a distance R
P0 = Power of the radar pulse at a reference distance
From the above equation, it can be observed that the power of the radar pulse is inversely proportional to the square of the range. Therefore, to double the range, the power of the radar pulse needs to be increased by a factor of 2² = 4.
However, we also need to consider that the transmit power is squared in the radar range equation:
R = (c * Δt) / 2
Therefore, to double the range, the transmit power needs to be increased by a factor of 4² = 16.
Hence, the correct answer is option 'D' - increased by a factor of 16.
To understand why the peak transmit power of the radar has to be increased by a factor of 16 when the range is doubled, we need to consider the basic principles of radar operation.
Radar Operation:
Radar works by transmitting a high-frequency electromagnetic wave, known as a radar pulse, and then detecting the echo reflected back from a target. The time taken for the pulse to travel to the target and return is used to calculate the range or distance to the target.
Radar Range Equation:
The range or distance to a target can be calculated using the radar range equation:
R = (c * Δt) / 2
Where:
R = Range to the target
c = Speed of light
Δt = Time taken for the pulse to travel to the target and return
Relationship between Transmit Power and Range:
In the radar range equation, the time taken for the pulse to travel to the target and return (Δt) is directly proportional to the range (R). This means that to increase the range, the time taken for the pulse to travel to the target and return must be increased.
The time taken for the pulse to travel to the target and return is determined by the speed of light (c) and the distance traveled by the pulse. Since the speed of light is constant, the distance traveled by the pulse needs to be increased to increase the time taken.
To increase the distance traveled by the pulse, the transmit power of the radar needs to be increased. This is because the power of the radar pulse decreases with distance due to spreading and attenuation effects.
Relationship between Transmit Power and Range:
The power of a radar pulse decreases with distance according to the inverse square law:
P = P0 / (4πR²)
Where:
P = Power of the radar pulse at a distance R
P0 = Power of the radar pulse at a reference distance
From the above equation, it can be observed that the power of the radar pulse is inversely proportional to the square of the range. Therefore, to double the range, the power of the radar pulse needs to be increased by a factor of 2² = 4.
However, we also need to consider that the transmit power is squared in the radar range equation:
R = (c * Δt) / 2
Therefore, to double the range, the transmit power needs to be increased by a factor of 4² = 16.
Hence, the correct answer is option 'D' - increased by a factor of 16.
Free Test
FREE
| Start Free Test |
Community Answer
If the range of a radar is to be doubled, the peak transmit power of t...
The range of the radar is given as:
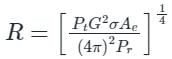
G = Antenna Gain
σ = Radar Cross-Section
Pr = Reflected Power
Ae = Effective Area of the Antenna
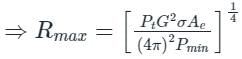
∴ Rmax ∝ (Pt)1/4
To double Rmax, Pt must be increased by a factor of 16

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Question Description
If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2025 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer?.
If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2025 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer?.
Solutions for If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electronics and Communication Engineering (ECE).
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Here you can find the meaning of If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer?, a detailed solution for If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If the range of a radar is to be doubled, the peak transmit power of the radar has to bea)increased by a factor of 2b)increased by a factor of 4c)decreased by a factor of 4d)increased by a factor of 16Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Electronics and Communication Engineering (ECE) tests.

|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















