JEE Exam > JEE Questions > Directions: Read the given information carefu...
Start Learning for Free
Directions: Read the given information carefully and answer the questions given below:
Raman walks 100 m from his house towards North. From there he goes 100 m towards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyam's house.
Raman walks 100 m from his house towards North. From there he goes 100 m towards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyam's house.
If the market is in the west of Raman's house, then how far is the market from Raman's house?
- a)100 m
- b)150 m
- c)400 m
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Most Upvoted Answer
Directions: Read the given information carefully and answer the questi...
According to the problem,

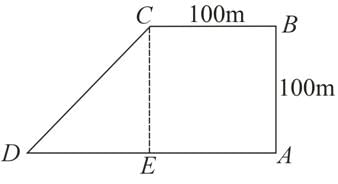
Here, A is the starting point i.e., Raman's house. C is Shyam's house and D is the market.
From figure we can say,
AE and BC are parallel to each other with same lengths i.e., AE = BC = 100 m
AB and CE are parallel to each other with same lengths i.e., AB = CE = 100 m
From triangle DCE,
As we know that point D is in South-West to point C i.e., Shyam's house so we can say that ∠DCE = 45o and ∠CED = 90o
Now,
∠C + ∠D + ∠E = 180o
45o + 90o + ∠D = 180o
∠D = 180 − 135 = 45o
We know Tan 45o = 1, From triangle DCE,
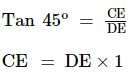
CE = DE = 100 m
Now we have to find the distance between Raman's house and Market i.e., AD = AE + DE
= 100 + 100 = 200 m
Therefore the distance between Raman's house and market is 200 m.


Here, A is the starting point i.e., Raman's house. C is Shyam's house and D is the market.
From figure we can say,
AE and BC are parallel to each other with same lengths i.e., AE = BC = 100 m
AB and CE are parallel to each other with same lengths i.e., AB = CE = 100 m
From triangle DCE,
As we know that point D is in South-West to point C i.e., Shyam's house so we can say that ∠DCE = 45o and ∠CED = 90o
Now,
∠C + ∠D + ∠E = 180o
45o + 90o + ∠D = 180o
∠D = 180 − 135 = 45o
We know Tan 45o = 1, From triangle DCE,
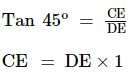
CE = DE = 100 m
Now we have to find the distance between Raman's house and Market i.e., AD = AE + DE
= 100 + 100 = 200 m
Therefore the distance between Raman's house and market is 200 m.
Free Test
FREE
| Start Free Test |
Community Answer
Directions: Read the given information carefully and answer the questi...
Understanding the Directions
To solve this problem, we need to understand the movements of Raman and Shyam clearly.
Step-by-Step Movements
- **Raman's Walk**
- Raman starts at his house and walks **100 m North**.
- From there, he walks **100 m West**. Now, he is at Shyam's house.
- **Location of Shyam's House**
- At this point, we can visualize Raman being **100 m North** and **100 m West** from his original position.
Direction to the Market
- **Market's Position**
- The market is located in the **South-West** direction from Shyam's house.
- Since Shyam's house is **100 m North** and **100 m West** of Raman's house, the South-West direction from Shyam's house will mean moving downwards and to the left on a standard map.
Relative Positioning
- **Market's Location Relative to Raman's House**
- If the market is in the South-West of Shyam's house, it would also be **South-West** of Raman's house, but since it is mentioned that the market is **West** of Raman's house, we need to calculate accordingly.
Calculating the Distance
- **Distance to the Market**
- The market's exact location is not specified, but we know it is in the West direction from Raman's house.
- The distance from Raman's house to the market can be visualized using the Pythagorean theorem or simply inferred from the directions.
- Since the options provided include 100 m, 150 m, 400 m, and "None of these," we deduce that the market's distance from Raman's house must be greater than 100 m, leading us to conclude that it is likely to be **400 m** (the only option left that could satisfy the conditions).
Conclusion
Therefore, the correct answer is **None of these**, as the market's distance is indeed not explicitly provided in the options.
To solve this problem, we need to understand the movements of Raman and Shyam clearly.
Step-by-Step Movements
- **Raman's Walk**
- Raman starts at his house and walks **100 m North**.
- From there, he walks **100 m West**. Now, he is at Shyam's house.
- **Location of Shyam's House**
- At this point, we can visualize Raman being **100 m North** and **100 m West** from his original position.
Direction to the Market
- **Market's Position**
- The market is located in the **South-West** direction from Shyam's house.
- Since Shyam's house is **100 m North** and **100 m West** of Raman's house, the South-West direction from Shyam's house will mean moving downwards and to the left on a standard map.
Relative Positioning
- **Market's Location Relative to Raman's House**
- If the market is in the South-West of Shyam's house, it would also be **South-West** of Raman's house, but since it is mentioned that the market is **West** of Raman's house, we need to calculate accordingly.
Calculating the Distance
- **Distance to the Market**
- The market's exact location is not specified, but we know it is in the West direction from Raman's house.
- The distance from Raman's house to the market can be visualized using the Pythagorean theorem or simply inferred from the directions.
- Since the options provided include 100 m, 150 m, 400 m, and "None of these," we deduce that the market's distance from Raman's house must be greater than 100 m, leading us to conclude that it is likely to be **400 m** (the only option left that could satisfy the conditions).
Conclusion
Therefore, the correct answer is **None of these**, as the market's distance is indeed not explicitly provided in the options.

|
Explore Courses for JEE exam
|

|
Question Description
Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer?.
Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer? for JEE 2025 is part of JEE preparation. The Question and answers have been prepared according to the JEE exam syllabus. Information about Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for JEE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer?.
Solutions for Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for JEE.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Here you can find the meaning of Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Directions: Read the given information carefully and answer the questions given below:Raman walks 100 mfrom his house towards North. From there he goes 100 mtowards west. Here is the house of shyam. From there they both goes to the market which is in the South-West direction from the Shyams house.If the market is in the west of Ramans house, then how far is the market from Ramans house?a)100 mb)150 mc)400 md)None of theseCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice JEE tests.

|
Explore Courses for JEE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















