ACT Exam > ACT Questions > If2sinθ/cos3θ = tan 270° - ta...
Start Learning for Free
If 2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?
- a)45°
- b)135°
- c)100°
- d)90°
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
If2sinθ/cos3θ = tan 270° - tan θ, find the value...
Formula:
sin2θ = 2sinθcosθ
sin(A - B) = sinAcosB - cosAsinB
sin2θ = 2sinθcosθ
sin(A - B) = sinAcosB - cosAsinB
Calculation:
Multiplying the left hand side with cosθ, we get-
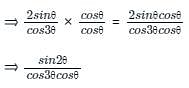
Multiplying the left hand side with cosθ, we get-
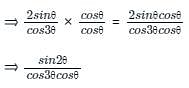
sin2θ can also be written as sin(3θ - θ)
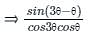
Applying sin(A-B) formula in the numerator part, we get-
⇒ tan3θ - tanθ
Equating LHS with RHS, we get-
⇒ tan3θ - tanθ = tan 270° - tan θ
⇒ 3θ = 270°
⇒ θ = 90°
∴ The value of θ is 90°
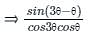
Applying sin(A-B) formula in the numerator part, we get-
⇒ tan3θ - tanθ
Equating LHS with RHS, we get-
⇒ tan3θ - tanθ = tan 270° - tan θ
⇒ 3θ = 270°
⇒ θ = 90°
∴ The value of θ is 90°
Most Upvoted Answer
If2sinθ/cos3θ = tan 270° - tan θ, find the value...
Understanding the Equation
We start with the equation:
2sinθ / cos3θ = tan 270° - tan θ
First, let's analyze the right side of the equation:
tan 270° Calculation
- tan 270° is undefined because it corresponds to a vertical asymptote in the tangent function.
- Therefore, we rewrite the equation as:
2sinθ / cos3θ = -tan θ
Rearranging the Equation
Now we can rearrange the equation:
- Multiply both sides by cos3θ to eliminate the fraction:
2sinθ = -tan θ * cos3θ
- Recall that tan θ = sinθ / cosθ, so we can substitute:
2sinθ = - (sinθ / cosθ) * cos3θ
Simplifying the Terms
- Multiplying both sides by cosθ gives us:
2sinθ * cosθ = -sinθ * cos3θ
- Dividing both sides by sinθ (assuming sinθ ≠ 0):
2cosθ = -cos3θ
Using the Cosine Triple Angle Identity
Now we can apply the cosine triple angle identity:
- cos3θ = 4cos^3θ - 3cosθ
Substituting this into the equation gives:
2cosθ = - (4cos^3θ - 3cosθ)
Final Rearrangement
- Rearranging yields:
4cos^3θ - 5cosθ = 0
- Factoring out cosθ:
cosθ(4cos^2θ - 5) = 0
This results in two cases:
1. cosθ = 0 → θ = 90° (which is the answer)
2. 4cos^2θ - 5 = 0 → cos^2θ = 5/4 (not valid since cos² cannot exceed 1)
Conclusion
The only valid solution is:
- θ = 90°
Thus, the answer is option 'D' (90°).
We start with the equation:
2sinθ / cos3θ = tan 270° - tan θ
First, let's analyze the right side of the equation:
tan 270° Calculation
- tan 270° is undefined because it corresponds to a vertical asymptote in the tangent function.
- Therefore, we rewrite the equation as:
2sinθ / cos3θ = -tan θ
Rearranging the Equation
Now we can rearrange the equation:
- Multiply both sides by cos3θ to eliminate the fraction:
2sinθ = -tan θ * cos3θ
- Recall that tan θ = sinθ / cosθ, so we can substitute:
2sinθ = - (sinθ / cosθ) * cos3θ
Simplifying the Terms
- Multiplying both sides by cosθ gives us:
2sinθ * cosθ = -sinθ * cos3θ
- Dividing both sides by sinθ (assuming sinθ ≠ 0):
2cosθ = -cos3θ
Using the Cosine Triple Angle Identity
Now we can apply the cosine triple angle identity:
- cos3θ = 4cos^3θ - 3cosθ
Substituting this into the equation gives:
2cosθ = - (4cos^3θ - 3cosθ)
Final Rearrangement
- Rearranging yields:
4cos^3θ - 5cosθ = 0
- Factoring out cosθ:
cosθ(4cos^2θ - 5) = 0
This results in two cases:
1. cosθ = 0 → θ = 90° (which is the answer)
2. 4cos^2θ - 5 = 0 → cos^2θ = 5/4 (not valid since cos² cannot exceed 1)
Conclusion
The only valid solution is:
- θ = 90°
Thus, the answer is option 'D' (90°).
Free Test
FREE
| Start Free Test |
Community Answer
If2sinθ/cos3θ = tan 270° - tan θ, find the value...
Formula:
sin2θ = 2sinθcosθ
sin(A - B) = sinAcosB - cosAsinB
sin2θ = 2sinθcosθ
sin(A - B) = sinAcosB - cosAsinB
Calculation:
Multiplying the left hand side with cosθ, we get-
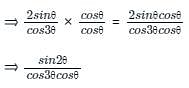
Multiplying the left hand side with cosθ, we get-
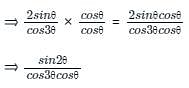
sin2θ can also be written as sin(3θ - θ)
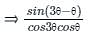
Applying sin(A-B) formula in the numerator part, we get-
⇒ tan3θ - tanθ
Equating LHS with RHS, we get-
⇒ tan3θ - tanθ = tan 270° - tan θ
⇒ 3θ = 270°
⇒ θ = 90°
∴ The value of θ is 90°
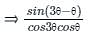
Applying sin(A-B) formula in the numerator part, we get-
⇒ tan3θ - tanθ
Equating LHS with RHS, we get-
⇒ tan3θ - tanθ = tan 270° - tan θ
⇒ 3θ = 270°
⇒ θ = 90°
∴ The value of θ is 90°
|
Explore Courses for ACT exam
|
|
Similar ACT Doubts
Top Courses for ACTView all
If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer?
Question Description
If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer? for ACT 2025 is part of ACT preparation. The Question and answers have been prepared according to the ACT exam syllabus. Information about If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for ACT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer?.
If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer? for ACT 2025 is part of ACT preparation. The Question and answers have been prepared according to the ACT exam syllabus. Information about If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for ACT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer?.
Solutions for If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for ACT.
Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.
Here you can find the meaning of If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer?, a detailed solution for If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?a)45°b)135°c)100°d)90°Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice ACT tests.
|
|
Explore Courses for ACT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup