GMAT Exam > GMAT Questions > Two trains left from two stations P and Q tow...
Start Learning for Free
Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?
- a)18h
- b)25h
- c)36h
- d)45h
- e)48h
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
Two trains left from two stations P and Q towards station Q and statio...
Let's assume that the first train's speed is x km/h and the second train's speed is y km/h.
Meeting Point:
When the two trains meet, they have traveled a total of 675 km. Since the first train has traveled for 3 hours more than the second train, we can use the formula Distance = Speed * Time to find the distance traveled by each train.
- The distance traveled by the first train is 3 hours * x km/h = 3x km.
- The distance traveled by the second train is y km/h * (3 hours - 0 hours) = 3y km.
Total Distance Traveled:
After their meeting, the two trains continue to travel to their respective destinations. We know that the first train arrives at its destination 16 hours after the meeting and the second train arrives 25 hours after the meeting. We can use the same formula Distance = Speed * Time to find the total distance traveled by each train.
- The total distance traveled by the first train is x km/h * (3 hours + 16 hours) = 19x km.
- The total distance traveled by the second train is y km/h * (3 hours + 25 hours) = 28y km.
Since the total distance traveled by both trains adds up to 675 km, we can write the equation:
19x + 28y = 675
To find the time it takes for the first train to make the whole trip, we need to find x. From the given options, we can substitute each answer choice for x and see which one satisfies the equation.
- If we substitute 18 for x, we get 19(18) + 28y = 675, which is not true.
- If we substitute 25 for x, we get 19(25) + 28y = 675, which is not true.
- If we substitute 36 for x, we get 19(36) + 28y = 675, which is not true.
- If we substitute 45 for x, we get 19(45) + 28y = 675, which is not true.
- If we substitute 48 for x, we get 19(48) + 28y = 675, which is true.
Therefore, the correct answer is option C) 36 hours, as it satisfies the equation and represents the time it takes for the first train to make the whole trip.
Meeting Point:
When the two trains meet, they have traveled a total of 675 km. Since the first train has traveled for 3 hours more than the second train, we can use the formula Distance = Speed * Time to find the distance traveled by each train.
- The distance traveled by the first train is 3 hours * x km/h = 3x km.
- The distance traveled by the second train is y km/h * (3 hours - 0 hours) = 3y km.
Total Distance Traveled:
After their meeting, the two trains continue to travel to their respective destinations. We know that the first train arrives at its destination 16 hours after the meeting and the second train arrives 25 hours after the meeting. We can use the same formula Distance = Speed * Time to find the total distance traveled by each train.
- The total distance traveled by the first train is x km/h * (3 hours + 16 hours) = 19x km.
- The total distance traveled by the second train is y km/h * (3 hours + 25 hours) = 28y km.
Since the total distance traveled by both trains adds up to 675 km, we can write the equation:
19x + 28y = 675
To find the time it takes for the first train to make the whole trip, we need to find x. From the given options, we can substitute each answer choice for x and see which one satisfies the equation.
- If we substitute 18 for x, we get 19(18) + 28y = 675, which is not true.
- If we substitute 25 for x, we get 19(25) + 28y = 675, which is not true.
- If we substitute 36 for x, we get 19(36) + 28y = 675, which is not true.
- If we substitute 45 for x, we get 19(45) + 28y = 675, which is not true.
- If we substitute 48 for x, we get 19(48) + 28y = 675, which is true.
Therefore, the correct answer is option C) 36 hours, as it satisfies the equation and represents the time it takes for the first train to make the whole trip.
Free Test
FREE
| Start Free Test |
Community Answer
Two trains left from two stations P and Q towards station Q and statio...
Total distance travelled by both the trains before meeting = D
This distance will be covered in proportion of their speeds.
3 hours after meeting distance travelled by
A = 3 × SA
B = 3 × SB
3SA + 3SB = 675
SA + SB = 225
Remaining distance to be covered by 1st train =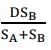
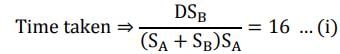
Remaining Distance covered by second train =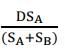
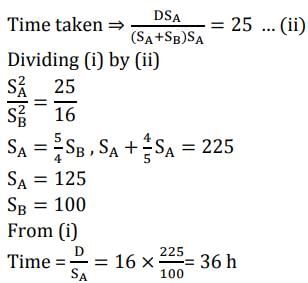
This distance will be covered in proportion of their speeds.
3 hours after meeting distance travelled by
A = 3 × SA
B = 3 × SB
3SA + 3SB = 675
SA + SB = 225
Remaining distance to be covered by 1st train =
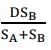
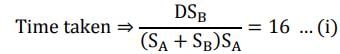
Remaining Distance covered by second train =
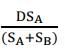
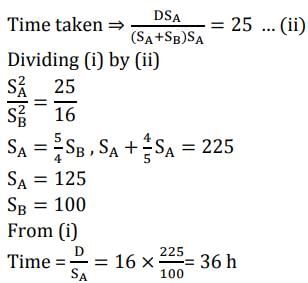

|
Explore Courses for GMAT exam
|

|
Similar GMAT Doubts
Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer?
Question Description
Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer?.
Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Two trains left from two stations P and Q towards station Q and station P respectively. 3 hours after they met, they were 675 Km apart. First train arrived at its destination 16 hours after their meeting and the second train arrived at its destination 25 hours after their meeting. How long did it take for the first train to make the whole trip?a)18hb)25hc)36hd)45he)48hCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice GMAT tests.

|
Explore Courses for GMAT exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























