SSC CGL Exam > SSC CGL Questions > By which least number should 5000 be divided ...
Start Learning for Free
By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)
- a)2
- b)5
- c)10
- d)25
Correct answer is option 'A'. Can you explain this answer?
Most Upvoted Answer
By which least number should 5000 be divided so that it becomes a perf...
Problem:
By which least number should 5000 be divided so that it becomes a perfect square?
Solution:
To find the least number by which 5000 should be divided to become a perfect square, we need to analyze the prime factors of 5000.
Prime Factorization of 5000:
To find the prime factors of 5000, we can divide it successively by prime numbers until the quotient becomes 1.
5000 ÷ 2 = 2500
2500 ÷ 2 = 1250
1250 ÷ 2 = 625
625 ÷ 5 = 125
125 ÷ 5 = 25
25 ÷ 5 = 5
5 ÷ 5 = 1
Therefore, the prime factorization of 5000 is 2 × 2 × 2 × 5 × 5 × 5 × 5.
Perfect Square:
A number is a perfect square if all its prime factors occur in pairs. In other words, each prime factor should have an even exponent.
In the prime factorization of 5000, we have three 2's and four 5's. To make 5000 a perfect square, we need to pair these prime factors.
Pairing Prime Factors:
Since we have three 2's, we can pair them to get one 2 with an exponent of 2 (2^2).
For the remaining prime factors, we have four 5's. We can pair two of them to get one 5 with an exponent of 2 (5^2).
Now, we have 2^2 × 5^2 = 4 × 25 = 100.
Therefore, the least number by which 5000 should be divided to become a perfect square is 100.
Checking the Options:
Now let's check the options given in the question.
a) 2: 5000 ÷ 2 = 2500 (not a perfect square)
b) 5: 5000 ÷ 5 = 1000 (not a perfect square)
c) 10: 5000 ÷ 10 = 500 (not a perfect square)
d) 25: 5000 ÷ 25 = 200 (not a perfect square)
Since none of the options except option 'A' (2) result in a perfect square, the correct answer is option 'A'.
By which least number should 5000 be divided so that it becomes a perfect square?
Solution:
To find the least number by which 5000 should be divided to become a perfect square, we need to analyze the prime factors of 5000.
Prime Factorization of 5000:
To find the prime factors of 5000, we can divide it successively by prime numbers until the quotient becomes 1.
5000 ÷ 2 = 2500
2500 ÷ 2 = 1250
1250 ÷ 2 = 625
625 ÷ 5 = 125
125 ÷ 5 = 25
25 ÷ 5 = 5
5 ÷ 5 = 1
Therefore, the prime factorization of 5000 is 2 × 2 × 2 × 5 × 5 × 5 × 5.
Perfect Square:
A number is a perfect square if all its prime factors occur in pairs. In other words, each prime factor should have an even exponent.
In the prime factorization of 5000, we have three 2's and four 5's. To make 5000 a perfect square, we need to pair these prime factors.
Pairing Prime Factors:
Since we have three 2's, we can pair them to get one 2 with an exponent of 2 (2^2).
For the remaining prime factors, we have four 5's. We can pair two of them to get one 5 with an exponent of 2 (5^2).
Now, we have 2^2 × 5^2 = 4 × 25 = 100.
Therefore, the least number by which 5000 should be divided to become a perfect square is 100.
Checking the Options:
Now let's check the options given in the question.
a) 2: 5000 ÷ 2 = 2500 (not a perfect square)
b) 5: 5000 ÷ 5 = 1000 (not a perfect square)
c) 10: 5000 ÷ 10 = 500 (not a perfect square)
d) 25: 5000 ÷ 25 = 200 (not a perfect square)
Since none of the options except option 'A' (2) result in a perfect square, the correct answer is option 'A'.
Free Test
FREE
| Start Free Test |
Community Answer
By which least number should 5000 be divided so that it becomes a perf...
According to option,
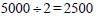
Hence, 2500 is a perfect square of 50.
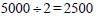
Hence, 2500 is a perfect square of 50.

|
Explore Courses for SSC CGL exam
|

|
Question Description
By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer? for SSC CGL 2025 is part of SSC CGL preparation. The Question and answers have been prepared according to the SSC CGL exam syllabus. Information about By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC CGL 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer?.
By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer? for SSC CGL 2025 is part of SSC CGL preparation. The Question and answers have been prepared according to the SSC CGL exam syllabus. Information about By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC CGL 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer?.
Solutions for By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC CGL.
Download more important topics, notes, lectures and mock test series for SSC CGL Exam by signing up for free.
Here you can find the meaning of By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer?, a detailed solution for By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice By which least number should 5000 be divided so that it becomes a perfect square? (SSC CGL 2017)a)2b)5c)10d)25Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice SSC CGL tests.

|
Explore Courses for SSC CGL exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.