GRE Exam > GRE Questions > Directions: Compare Quantity A and Quantity ...
Start Learning for Free
Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.
Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.
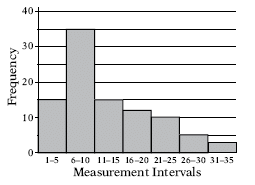
Quantity A: The average (arithmetic mean) of the 95 measurements
Quantity B: The median of the 95 measurements
(d)The relationship cannot be determined from the information given.
- a)Quantity A is greater.
- b)Quantity B is greater.
- c)The two quantities are equal.
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
Directions: Compare Quantity A and Quantity B, using additional infor...
From the histogram, you can observe that 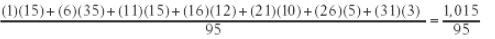
View all questions of this test
- all of the measurement intervals are the same size,
- the distribution has a peak at the measurement interval 6–10, and
- more of the measurement intervals are to the right of the peak than are to the left of the peak.
Since in the histogram the 95 measurements have been grouped into intervals, you cannot calculate the exact value of either the average or the median; you must compare them without being able to determine the exact value of either one.
The median of the 95 measurements is the middle measurement when the measurements are listed in increasing order. The middle measurement is the 48th measurement. From the histogram, you can see that the measurement interval 1–5 contains the first 15 measurements, and the measurement interval 6–10 contains the next 35 measurements (that is, measurements 16 through 50). Therefore, the median is in the measurement interval 6–10 and could be 6, 7, 8, 9, or 10.
Estimating the average of the 95 measurements is more complicated.
Since you are asked to compare the average and the median, not necessarily to calculate them, you may ask yourself if you can tell whether the average is greater than or less than the median. Note that visually the measurements in the first three measurement intervals are symmetric around the measurement interval 6–10, so you would expect the average of the measurements in just these three measurement intervals to lie in the 6–10 measurement interval. The 30 measurements in the remaining four measurement intervals are all greater than 10, some significantly greater than 10. Therefore, the average of the 95 measurements is greater than the average of the measurements in the first three measurement intervals, probably greater than 10. At this point it seems likely that the average of the 95 measurements is greater than the median of the 95 measurements. It turns out that this is true.
To actually show that the average must be greater than 10, you can make the average as small as possible and see if the smallest possible average is greater than 10. To make the average as small as possible, assume that all of the measurements in each interval are as small as possible. That is to say, all 15 measurements in the measurement interval 1–5 are equal to 1, all 35 measurements in the measurement interval 6–10 are equal to 6, etc. Under this assumption, the average of the 95 measurements is
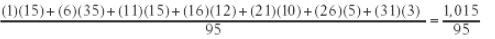
The value of the smallest possible average, 1,015/95 , is greater than 10.
Therefore, since the average of the 95 measurements is greater than 10 and the median is in the measurement interval 6–10, it follows that the average is greater than the median, and the correct answer is Choice A.
Most Upvoted Answer
Directions: Compare Quantity A and Quantity B, using additional infor...
From the histogram, you can observe that 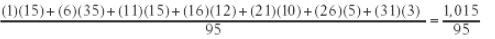
- all of the measurement intervals are the same size,
- the distribution has a peak at the measurement interval 6–10, and
- more of the measurement intervals are to the right of the peak than are to the left of the peak.
Since in the histogram the 95 measurements have been grouped into intervals, you cannot calculate the exact value of either the average or the median; you must compare them without being able to determine the exact value of either one.
The median of the 95 measurements is the middle measurement when the measurements are listed in increasing order. The middle measurement is the 48th measurement. From the histogram, you can see that the measurement interval 1–5 contains the first 15 measurements, and the measurement interval 6–10 contains the next 35 measurements (that is, measurements 16 through 50). Therefore, the median is in the measurement interval 6–10 and could be 6, 7, 8, 9, or 10.
Estimating the average of the 95 measurements is more complicated.
Since you are asked to compare the average and the median, not necessarily to calculate them, you may ask yourself if you can tell whether the average is greater than or less than the median. Note that visually the measurements in the first three measurement intervals are symmetric around the measurement interval 6–10, so you would expect the average of the measurements in just these three measurement intervals to lie in the 6–10 measurement interval. The 30 measurements in the remaining four measurement intervals are all greater than 10, some significantly greater than 10. Therefore, the average of the 95 measurements is greater than the average of the measurements in the first three measurement intervals, probably greater than 10. At this point it seems likely that the average of the 95 measurements is greater than the median of the 95 measurements. It turns out that this is true.
To actually show that the average must be greater than 10, you can make the average as small as possible and see if the smallest possible average is greater than 10. To make the average as small as possible, assume that all of the measurements in each interval are as small as possible. That is to say, all 15 measurements in the measurement interval 1–5 are equal to 1, all 35 measurements in the measurement interval 6–10 are equal to 6, etc. Under this assumption, the average of the 95 measurements is
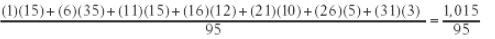
The value of the smallest possible average, 1,015/95 , is greater than 10.
Therefore, since the average of the 95 measurements is greater than 10 and the median is in the measurement interval 6–10, it follows that the average is greater than the median, and the correct answer is Choice A.
Free Test
FREE
| Start Free Test |
Community Answer
Directions: Compare Quantity A and Quantity B, using additional infor...
From the histogram, you can observe that 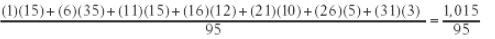
- all of the measurement intervals are the same size,
- the distribution has a peak at the measurement interval 6–10, and
- more of the measurement intervals are to the right of the peak than are to the left of the peak.
Since in the histogram the 95 measurements have been grouped into intervals, you cannot calculate the exact value of either the average or the median; you must compare them without being able to determine the exact value of either one.
The median of the 95 measurements is the middle measurement when the measurements are listed in increasing order. The middle measurement is the 48th measurement. From the histogram, you can see that the measurement interval 1–5 contains the first 15 measurements, and the measurement interval 6–10 contains the next 35 measurements (that is, measurements 16 through 50). Therefore, the median is in the measurement interval 6–10 and could be 6, 7, 8, 9, or 10.
Estimating the average of the 95 measurements is more complicated.
Since you are asked to compare the average and the median, not necessarily to calculate them, you may ask yourself if you can tell whether the average is greater than or less than the median. Note that visually the measurements in the first three measurement intervals are symmetric around the measurement interval 6–10, so you would expect the average of the measurements in just these three measurement intervals to lie in the 6–10 measurement interval. The 30 measurements in the remaining four measurement intervals are all greater than 10, some significantly greater than 10. Therefore, the average of the 95 measurements is greater than the average of the measurements in the first three measurement intervals, probably greater than 10. At this point it seems likely that the average of the 95 measurements is greater than the median of the 95 measurements. It turns out that this is true.
To actually show that the average must be greater than 10, you can make the average as small as possible and see if the smallest possible average is greater than 10. To make the average as small as possible, assume that all of the measurements in each interval are as small as possible. That is to say, all 15 measurements in the measurement interval 1–5 are equal to 1, all 35 measurements in the measurement interval 6–10 are equal to 6, etc. Under this assumption, the average of the 95 measurements is
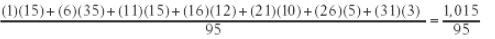
The value of the smallest possible average, 1,015/95 , is greater than 10.
Therefore, since the average of the 95 measurements is greater than 10 and the median is in the measurement interval 6–10, it follows that the average is greater than the median, and the correct answer is Choice A.

|
Explore Courses for GRE exam
|

|
Question Description
Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer? for GRE 2025 is part of GRE preparation. The Question and answers have been prepared according to the GRE exam syllabus. Information about Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for GRE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer?.
Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer? for GRE 2025 is part of GRE preparation. The Question and answers have been prepared according to the GRE exam syllabus. Information about Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for GRE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer?.
Solutions for Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for GRE.
Download more important topics, notes, lectures and mock test series for GRE Exam by signing up for free.
Here you can find the meaning of Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer?, a detailed solution for Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Directions: Compare Quantity A and Quantity B, using additional information centered above the two quantities if such information is given. Select one of the following four answer choices. A symbol that appears more than once in a question has the same meaning throughout the question.Q. In the course of an experiment, 95 measurements were recorded, and all of the measurements were integers. The 95 measurements were then grouped into 7 measurement intervals. The graph below shows the frequency distribution of the 95 measurements by measurement interval.Quantity A: The average (arithmetic mean) of the 95 measurementsQuantity B: The median of the 95 measurements(d)The relationship cannot be determined from the information given.a)Quantity A is greater.b)Quantity B is greater.c)The two quantities are equal.Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice GRE tests.

|
Explore Courses for GRE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















