Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > Let A be an n × n complex matrix. Assum...
Start Learning for Free
Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B are
- a)purely imaginary
- b)of modulus one
- c)real
- d)of modulus less than one
Correct answer is option 'B'. Can you explain this answer?
Most Upvoted Answer
Let A be an n × n complex matrix. Assume that A is self-adjoint ...
Concept:
(i) A complex matrix A is said to be self-adjoint if A = A* where A* = A-T
(ii) Eigenvalues of a self-adjoint matrix are real
Explanation:
A is an n × n complex matrix and A is self-adjoint so
A = A*
B denotes the inverse of (A + iIn).
So B = (A + iIn)-1
Let λ be an eigenvalue of A
then λ + i is an eigenvalue of A + iIn
and (λ + i)-1 is an eigenvalue of B
Also λ - i is an eigenvalue of A - iIn
Hence eigenvalue of (A - iIn)B
= (λ - i)(λ + i)-1
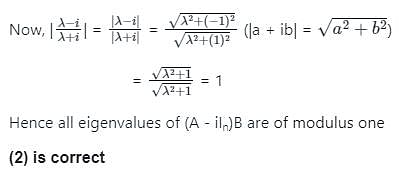
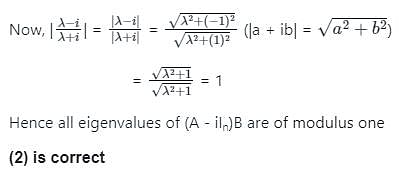
Community Answer
Let A be an n × n complex matrix. Assume that A is self-adjoint ...
× n matrix. The inverse of A, denoted as A^(-1), is a matrix such that the product of A and A^(-1) is equal to the identity matrix, denoted as I. In other words, if A is multiplied by its inverse, it results in the identity matrix.
The inverse of a matrix exists only if the matrix is square (i.e., the number of rows is equal to the number of columns) and if its determinant is non-zero. If these conditions are met, then the matrix is said to be invertible or non-singular.
To find the inverse of a matrix, various methods can be used, such as the Gauss-Jordan elimination method, the adjugate method, or using matrix algebra. The specific method used depends on the size of the matrix and the desired result.
In practical terms, finding the inverse of a matrix is useful in solving systems of linear equations, as it allows for the direct solution of the system using matrix multiplication. Additionally, the inverse of a matrix can be used to find the coefficient matrix in a system of equations when the solution vector is known.
The inverse of a matrix exists only if the matrix is square (i.e., the number of rows is equal to the number of columns) and if its determinant is non-zero. If these conditions are met, then the matrix is said to be invertible or non-singular.
To find the inverse of a matrix, various methods can be used, such as the Gauss-Jordan elimination method, the adjugate method, or using matrix algebra. The specific method used depends on the size of the matrix and the desired result.
In practical terms, finding the inverse of a matrix is useful in solving systems of linear equations, as it allows for the direct solution of the system using matrix multiplication. Additionally, the inverse of a matrix can be used to find the coefficient matrix in a system of equations when the solution vector is known.
|
Explore Courses for Civil Engineering (CE) exam
|
|
Similar Civil Engineering (CE) Doubts
Top Courses for Civil Engineering (CE)View all
Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer?
Question Description
Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer?.
Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer?.
Solutions for Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Let A be an n × n complex matrix. Assume that A is self-adjoint and let B denotes the inverse of (A + iIn). Then all eigenvalues of (A - iIn)B area)purely imaginaryb)of modulus onec)reald)of modulus less than oneCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.
|
|
Explore Courses for Civil Engineering (CE) exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup