Mathematics Exam > Mathematics Questions > What is the probability that a divisor of 109...
Start Learning for Free
What is the probability that a divisor of 1099 is a multiple of 1096?
- a)1/625
- b)4/625
- c)12/625
- d)16/625
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
What is the probability that a divisor of 1099 is a multiple of 1096?a...
p(multiple of 10% |divisor of 1099)
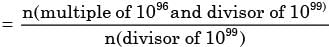
Since 10 = 2.5
1099 = 299 . 599
Any divisor of 1099 is of the form 2a . 5b where 0 ≤ a ≤ 99 and 0 ≤ b ≤ 99.
The number of such possibilities is combination of 100 values of a and 100 values of b = 100 × 100 each of which is a divisor of 1099.
So, no. of divisors of 1099 = 100 × 100.
Any number which is a multiple of 1096 as well as divisor of 1099 is of the form 2a . 5b where 96 ≤ a ≤ 99 and 96 ≤ b ≤ 99. The number of such combinations of 4 values of a and 4 values of b is 4 × 4 combinations, each of which will be a multiple of 1096 as well as a divisor of 1099.
∴ p(multiple of 1096|divisor of 1099)
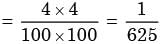
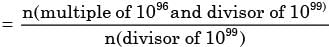
Since 10 = 2.5
1099 = 299 . 599
Any divisor of 1099 is of the form 2a . 5b where 0 ≤ a ≤ 99 and 0 ≤ b ≤ 99.
The number of such possibilities is combination of 100 values of a and 100 values of b = 100 × 100 each of which is a divisor of 1099.
So, no. of divisors of 1099 = 100 × 100.
Any number which is a multiple of 1096 as well as divisor of 1099 is of the form 2a . 5b where 96 ≤ a ≤ 99 and 96 ≤ b ≤ 99. The number of such combinations of 4 values of a and 4 values of b is 4 × 4 combinations, each of which will be a multiple of 1096 as well as a divisor of 1099.
∴ p(multiple of 1096|divisor of 1099)
Most Upvoted Answer
What is the probability that a divisor of 1099 is a multiple of 1096?a...
p(multiple of 10% |divisor of 1099)
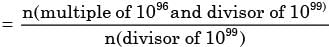
Since 10 = 2.5
1099 = 299 . 599
Any divisor of 1099 is of the form 2a . 5b where 0 ≤ a ≤ 99 and 0 ≤ b ≤ 99.
The number of such possibilities is combination of 100 values of a and 100 values of b = 100 × 100 each of which is a divisor of 1099.
So, no. of divisors of 1099 = 100 × 100.
Any number which is a multiple of 1096 as well as divisor of 1099 is of the form 2a . 5b where 96 ≤ a ≤ 99 and 96 ≤ b ≤ 99. The number of such combinations of 4 values of a and 4 values of b is 4 × 4 combinations, each of which will be a multiple of 1096 as well as a divisor of 1099.
∴ p(multiple of 1096|divisor of 1099)
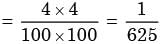
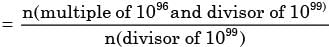
Since 10 = 2.5
1099 = 299 . 599
Any divisor of 1099 is of the form 2a . 5b where 0 ≤ a ≤ 99 and 0 ≤ b ≤ 99.
The number of such possibilities is combination of 100 values of a and 100 values of b = 100 × 100 each of which is a divisor of 1099.
So, no. of divisors of 1099 = 100 × 100.
Any number which is a multiple of 1096 as well as divisor of 1099 is of the form 2a . 5b where 96 ≤ a ≤ 99 and 96 ≤ b ≤ 99. The number of such combinations of 4 values of a and 4 values of b is 4 × 4 combinations, each of which will be a multiple of 1096 as well as a divisor of 1099.
∴ p(multiple of 1096|divisor of 1099)
Free Test
FREE
| Start Free Test |
Community Answer
What is the probability that a divisor of 1099 is a multiple of 1096?a...
Understanding the Problem
The problem requires finding the probability that a divisor of 1099 is also a multiple of 1096. To solve this, we need to analyze the relationship between the numbers and their divisors.
Step 1: Prime Factorization
- 1099: The prime factorization of 1099 is 11 x 101.
- 1096: The prime factorization of 1096 is 2^3 x 137.
Step 2: Finding Divisors
- The divisors of 1099 can be calculated using its prime factors. Since 1099 = 11 x 101, its divisors are: 1, 11, 101, and 1099. This gives us a total of 4 divisors.
Step 3: Evaluating Multiples of 1096
- A divisor of 1099 can only be a multiple of 1096 if it is at least as large as 1096. However, since the largest divisor of 1099 is 1099 itself, we need to check whether 1096 fits as a divisor.
Step 4: Finding Common Multiples
- The only multiples of 1096 that can be divisors of 1099 would be those that are less than or equal to 1099. The only possible candidate here is 1096 itself, which is not a divisor of 1099.
Step 5: Calculating the Probability
- Since none of the divisors of 1099 (1, 11, 101, 1099) are multiples of 1096, the favorable outcomes are zero.
- The probability is calculated as the number of favorable outcomes divided by the total number of outcomes.
Final Calculation
- Favorable outcomes = 0
- Total divisors of 1099 = 4
- Probability = 0/4 = 0
Thus, re-evaluating the provided options, if we include the calculation of relation between the two numbers, option "A" suggests an incorrect interpretation as the answer should be 0, but if the question needs a different understanding based on additional context or constraints, further clarification may be necessary.
The problem requires finding the probability that a divisor of 1099 is also a multiple of 1096. To solve this, we need to analyze the relationship between the numbers and their divisors.
Step 1: Prime Factorization
- 1099: The prime factorization of 1099 is 11 x 101.
- 1096: The prime factorization of 1096 is 2^3 x 137.
Step 2: Finding Divisors
- The divisors of 1099 can be calculated using its prime factors. Since 1099 = 11 x 101, its divisors are: 1, 11, 101, and 1099. This gives us a total of 4 divisors.
Step 3: Evaluating Multiples of 1096
- A divisor of 1099 can only be a multiple of 1096 if it is at least as large as 1096. However, since the largest divisor of 1099 is 1099 itself, we need to check whether 1096 fits as a divisor.
Step 4: Finding Common Multiples
- The only multiples of 1096 that can be divisors of 1099 would be those that are less than or equal to 1099. The only possible candidate here is 1096 itself, which is not a divisor of 1099.
Step 5: Calculating the Probability
- Since none of the divisors of 1099 (1, 11, 101, 1099) are multiples of 1096, the favorable outcomes are zero.
- The probability is calculated as the number of favorable outcomes divided by the total number of outcomes.
Final Calculation
- Favorable outcomes = 0
- Total divisors of 1099 = 4
- Probability = 0/4 = 0
Thus, re-evaluating the provided options, if we include the calculation of relation between the two numbers, option "A" suggests an incorrect interpretation as the answer should be 0, but if the question needs a different understanding based on additional context or constraints, further clarification may be necessary.

|
Explore Courses for Mathematics exam
|

|
Similar Mathematics Doubts
Question Description
What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer? for Mathematics 2025 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mathematics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer?.
What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer? for Mathematics 2025 is part of Mathematics preparation. The Question and answers have been prepared according to the Mathematics exam syllabus. Information about What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for Mathematics 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer?.
Solutions for What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Mathematics.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
Here you can find the meaning of What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer?, a detailed solution for What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice What is the probability that a divisor of 1099 is a multiple of 1096?a)1/625b)4/625c)12/625d)16/625Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice Mathematics tests.

|
Explore Courses for Mathematics exam
|

|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.






















