ACT Exam > ACT Questions > A system of linear equations is shown below.4...
Start Learning for Free
A system of linear equations is shown below.
4y - 2x = 8
4y + 2x = 8
Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?
4y - 2x = 8
4y + 2x = 8
Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?
- a)A single line with positive slope
- b)A single line with negative slope
- c)Two distinct intersecting lines
- d)Two parallel lines with positive slope
- e)Two parallel lines with negative slope
Correct answer is option 'C'. Can you explain this answer?
Most Upvoted Answer
A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Whic...
To solve this problem, it would be helpful to make the properties of both lines more evident by converting them to slope-intercept form (y = mx + b, where m is the slope and b is the y-intercept). To start, adding 2x to both sides and dividing both sides of the equation 4y - 2x = 8 by 4 yields y = x/2 + 2. Similarly, subtracting 2x from both sides and dividing both sides of the equation 4y + 2x = 8 by 4 yields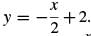 
. The relationship between 
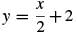and 
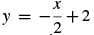is that they are lines that share the same y-intercept, yet they have opposite slopes 
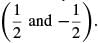Therefore these are two distinct intersecting lines.
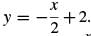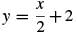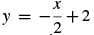. The relationship between and is that they are lines that share the same y-intercept, yet they have opposite slopes Therefore these are two distinct intersecting lines.Community Answer
A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Whic...
Graphical representation of a system of linear equations:
To determine the graph of the given system of linear equations, we can convert the equations into slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept. Let's rewrite the equations in this form:
Equation 1: 4y - 2x = 8
Rearranging the equation, we get:
4y = 2x + 8
y = (2/4)x + 2
y = (1/2)x + 2
Equation 2: 4y + 2x = 8
Rearranging the equation, we get:
4y = -2x + 8
y = (-2/4)x + 2
y = (-1/2)x + 2
From these equations, we can observe the following:
1. Slopes:
Equation 1 has a slope of 1/2 (positive slope).
Equation 2 has a slope of -1/2 (negative slope).
2. Y-intercepts:
Both equations have a y-intercept of 2.
Based on these observations, we can conclude that the graph of this system of linear equations consists of two distinct intersecting lines.
Explanation:
When we plot the graph of the first equation, y = (1/2)x + 2, we will find that it has a positive slope and a y-intercept at (0, 2). This line will pass through the points (2, 3), (4, 4), etc.
When we plot the graph of the second equation, y = (-1/2)x + 2, we will find that it has a negative slope and a y-intercept at (0, 2). This line will pass through the points (-2, 3), (-4, 4), etc.
Since the two lines have different slopes, they will intersect at a single point. This point represents the solution to the system of equations. In this case, the point of intersection is (4, 4).
Therefore, the correct answer is option C: Two distinct intersecting lines.
To determine the graph of the given system of linear equations, we can convert the equations into slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept. Let's rewrite the equations in this form:
Equation 1: 4y - 2x = 8
Rearranging the equation, we get:
4y = 2x + 8
y = (2/4)x + 2
y = (1/2)x + 2
Equation 2: 4y + 2x = 8
Rearranging the equation, we get:
4y = -2x + 8
y = (-2/4)x + 2
y = (-1/2)x + 2
From these equations, we can observe the following:
1. Slopes:
Equation 1 has a slope of 1/2 (positive slope).
Equation 2 has a slope of -1/2 (negative slope).
2. Y-intercepts:
Both equations have a y-intercept of 2.
Based on these observations, we can conclude that the graph of this system of linear equations consists of two distinct intersecting lines.
Explanation:
When we plot the graph of the first equation, y = (1/2)x + 2, we will find that it has a positive slope and a y-intercept at (0, 2). This line will pass through the points (2, 3), (4, 4), etc.
When we plot the graph of the second equation, y = (-1/2)x + 2, we will find that it has a negative slope and a y-intercept at (0, 2). This line will pass through the points (-2, 3), (-4, 4), etc.
Since the two lines have different slopes, they will intersect at a single point. This point represents the solution to the system of equations. In this case, the point of intersection is (4, 4).
Therefore, the correct answer is option C: Two distinct intersecting lines.
|
Explore Courses for ACT exam
|
|
Top Courses for ACTView all
A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer?
Question Description
A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer? for ACT 2025 is part of ACT preparation. The Question and answers have been prepared according to the ACT exam syllabus. Information about A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for ACT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer?.
A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer? for ACT 2025 is part of ACT preparation. The Question and answers have been prepared according to the ACT exam syllabus. Information about A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for ACT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for ACT.
Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.
Here you can find the meaning of A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A system of linear equations is shown below.4y - 2x = 84y + 2x = 8Which of the following describes the graph of this system of linear equations in the standard (x, y) coordinate plane?a)A single line with positive slopeb)A single line with negative slopec)Two distinct intersecting linesd)Two parallel lines with positive slopee)Two parallel lines with negative slopeCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice ACT tests.
|
|
Explore Courses for ACT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup