MCAT Exam > MCAT Questions > A submarine is inspecting the surface of the ...
Start Learning for Free
A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)
- a)19°
- b)29°
- c)39°
- d)49°
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
A submarine is inspecting the surface of the water with a laser that p...
This question is testing our understanding of total internal reflection. As the laser beam travels from water to air—that is, from a higher to a lower index of refraction—the angle of refraction increases. At the critical angle (θc), the angle of refraction becomes 90°; at this point, the refracted ray is parallel to the surface of the water. When the angle of incidence is greater than the critical angle, all the light is reflected back into the water. The question is asking for the critical angle:
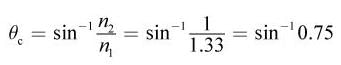
The inverse sine of 0.75 must be slightly higher than
48.59° is the exact answer.
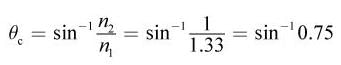
The inverse sine of 0.75 must be slightly higher than
48.59° is the exact answer.Most Upvoted Answer
A submarine is inspecting the surface of the water with a laser that p...
Understanding the concept:
When a laser beam travels from one medium to another, it can either be refracted, reflected, or transmitted depending on the angle of incidence and the refractive indices of the two media. In this case, the laser beam is traveling from the submarine through the air to the surface of the water.
Explanation:
To calculate the critical angle at which the laser beam will be totally internally reflected back into the water, we can use Snell's Law:
n1 * sin(theta1) = n2 * sin(theta2)
Given that n1 (refractive index of air) = 1 and n2 (refractive index of water) = 1.33, and since the laser beam will be totally internally reflected, the angle of refraction in air will be 90 degrees.
sin(theta1) = n2 / n1
sin(theta1) = 1.33 / 1
sin(theta1) = 1.33
Therefore, the critical angle theta1 = sin^(-1)(1.33) = 49 degrees.
Conclusion:
So, the angle at which the laser will not penetrate the surface of the water but rather reflect entirely back into the water is 49 degrees. This means that any angle greater than 49 degrees will result in total internal reflection of the laser beam.
|
Explore Courses for MCAT exam
|
|
Top Courses for MCATView all
Question Description
A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer? for MCAT 2025 is part of MCAT preparation. The Question and answers have been prepared according to the MCAT exam syllabus. Information about A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for MCAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer?.
A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer? for MCAT 2025 is part of MCAT preparation. The Question and answers have been prepared according to the MCAT exam syllabus. Information about A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for MCAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer?.
Solutions for A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for MCAT.
Download more important topics, notes, lectures and mock test series for MCAT Exam by signing up for free.
Here you can find the meaning of A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer?, a detailed solution for A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A submarine is inspecting the surface of the water with a laser that points from the submarine to the surface of the water and through the air. At what angle will the laser not penetrate the surface of the water but rather reflect entirely back into the water? (Assume nwater = 1.33 and nair = 1.)a)19°b)29°c)39°d)49°Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice MCAT tests.
|
|
Explore Courses for MCAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup