MCAT Exam > MCAT Questions > Which of the following vector combinations wi...
Start Learning for Free
Which of the following vector combinations will result in the least amount of displacement? (Note: Vectors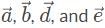 
have magnitudes double that of vectors 
have magnitudes double that of vectors - a)
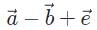
- b)
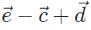
- c)
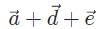
- d)
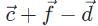
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
Which of the following vector combinations will result in the least am...
Let’s consider each case graphically to narrow down our choices. Recall that vectors 
are half the magnitude of vector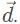 
By drawing out 
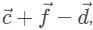we can see that the displacement is somewhat large:
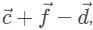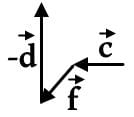
are half the magnitude of vector By drawing out we can see that the displacement is somewhat large:All three vectors have the same magnitude here. By drawing out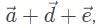 
, we can see that displacement is not large, but could be closer to zero:
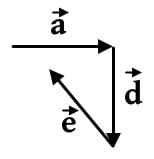
Between the remaining two, it becomes hard to discern visually which has the least displacement:
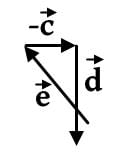
In analyzing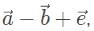
let’s pick 10 for the magnitude of each vector, and resolve all the vectors into the x and y direction. In a 45 − 45 − 90 triangle, remember that the sides are in a proportion of 1 : 1 : √2 so with the hypotenuse as 10 units, the x and y components are 5√2, units. In the x-direction, the x component vectors 
overlap and add up to 10 √2, which is opposed by vector 
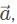, with, vector, on top, with a magnitude of 10.
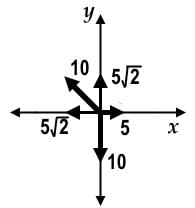
In the y-direction, the y-component of vectors
cancel each other out. The resultant vector points in the negative y-direction with an approximate magnitude of 4 since √2, is approximately equal to 1.4.
In analyzing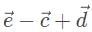
let’s pick 10 for the magnitude of vectors 
and 5 for the magnitude of vector 
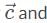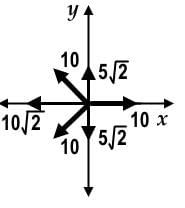
resolve all the vectors into the x and y components. Vector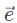 
resolves into an x and y components with magnitudes of 5√2 units:
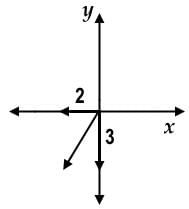
The resultant x-component is 2 in the negative-x direction, and the resultant y-component is 3 in the negative-y direction. To find our displacement, use the Pythagorean theorem to obtain √13 which is less than 4.
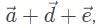, we can see that displacement is not large, but could be closer to zero:Between the remaining two, it becomes hard to discern visually which has the least displacement:
In analyzing
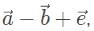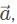let’s pick 10 for the magnitude of each vector, and resolve all the vectors into the x and y direction. In a 45 − 45 − 90 triangle, remember that the sides are in a proportion of 1 : 1 : √2 so with the hypotenuse as 10 units, the x and y components are 5√2, units. In the x-direction, the x component vectors overlap and add up to 10 √2, which is opposed by vector , with, vector, on top, with a magnitude of 10.In the y-direction, the y-component of vectors
cancel each other out. The resultant vector points in the negative y-direction with an approximate magnitude of 4 since √2, is approximately equal to 1.4.In analyzing
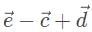let’s pick 10 for the magnitude of vectors and 5 for the magnitude of vector 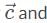resolve all the vectors into the x and y components. Vector 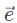resolves into an x and y components with magnitudes of 5√2 units:The resultant x-component is 2 in the negative-x direction, and the resultant y-component is 3 in the negative-y direction. To find our displacement, use the Pythagorean theorem to obtain √13 which is less than 4.
|
Explore Courses for MCAT exam
|
|
Top Courses for MCATView all
Question Description
Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer? for MCAT 2025 is part of MCAT preparation. The Question and answers have been prepared according to the MCAT exam syllabus. Information about Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for MCAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer?.
Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer? for MCAT 2025 is part of MCAT preparation. The Question and answers have been prepared according to the MCAT exam syllabus. Information about Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for MCAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer?.
Solutions for Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for MCAT.
Download more important topics, notes, lectures and mock test series for MCAT Exam by signing up for free.
Here you can find the meaning of Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following vector combinations will result in the least amount of displacement? (Note: Vectorshave magnitudes double that of vectorsa)b)c)d)Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice MCAT tests.
|
|
Explore Courses for MCAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup