MCAT Exam > MCAT Questions > Which of the following statements correctly i...
Start Learning for Free
Which of the following statements correctly identifies an example of the respective scalar or vector product processes?
I. Vector and scalar : torque
II. Vector and vector : magnetic force
III. Scalar and scalar : power
I. Vector and scalar : torque
II. Vector and vector : magnetic force
III. Scalar and scalar : power
- a)I and II
- b)III only
- c)II and III
- d)I only
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
Which of the following statements correctly identifies an example of t...
A scalar multiplied by a scalar will produce another scalar. For instance, distance divided by time is equal to speed, which is a scalar. In the case of power, energy divided by time is equal to power. Statement III is true.
A vector multiplied by a scalar is representative of the scalar product or the dot product and will always produce a vector. The scalar product of two vectors
can be constructed by taking the component of 
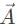in the direction of 
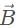and multiplying it times the magnitude of 
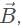and it can be expressed as AB cos θ.
A vector multiplied by a scalar is representative of the scalar product or the dot product and will always produce a vector. The scalar product of two vectors
can be constructed by taking the component of 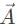in the direction of 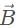and multiplying it times the magnitude of 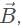and it can be expressed as AB cos θ.Torqueis not an example of the scalar product of vectors since it is equal to rF sinθ. A correct example of the dot product would be work, which is equal to Fd cos θ. Therefore, statement I is not true.
Vector multiplied by a vector is representative of the vector product or the cross product and will produce a vector or scalar. The magnitude of the vector product of
can be constructed by taking the product of the magnitudes of 
multiplied by the sine of the angle between them.
Magnetic force is an example of the vector cross product, so statement II is true. Therefore, the correct answer is that statements II and III are true.
Vector multiplied by a vector is representative of the vector product or the cross product and will produce a vector or scalar. The magnitude of the vector product of
can be constructed by taking the product of the magnitudes of multiplied by the sine of the angle between them.Magnetic force is an example of the vector cross product, so statement II is true. Therefore, the correct answer is that statements II and III are true.
Most Upvoted Answer
Which of the following statements correctly identifies an example of t...
Understanding Scalar and Vector Products
To clarify why option 'C' is correct, let's analyze the statements related to scalar and vector products.
Statement I: Vector and Scalar - Torque
- Torque is defined as the cross product of a vector (lever arm) and a force vector.
- It results in a vector quantity, not a scalar.
- Therefore, this statement is incorrect for identifying scalar or vector processes.
Statement II: Vector and Vector - Magnetic Force
- Magnetic force on a charged particle moving in a magnetic field is indeed a vector quantity.
- It is derived from the cross product of the velocity vector and the magnetic field vector.
- Hence, this statement correctly identifies a vector and vector process.
Statement III: Scalar and Scalar - Power
- Power is defined as the rate at which work is done or energy is transferred.
- It can be computed as the dot product of force (vector) and velocity (vector), resulting in a scalar quantity.
- Hence, this statement accurately identifies a scalar product.
Conclusion
Based on the analysis:
- I is incorrect.
- II is correct (Vector and Vector: Magnetic Force).
- III is also correct (Scalar and Scalar: Power).
Thus, the correct answer is option 'C' (II and III).
To clarify why option 'C' is correct, let's analyze the statements related to scalar and vector products.
Statement I: Vector and Scalar - Torque
- Torque is defined as the cross product of a vector (lever arm) and a force vector.
- It results in a vector quantity, not a scalar.
- Therefore, this statement is incorrect for identifying scalar or vector processes.
Statement II: Vector and Vector - Magnetic Force
- Magnetic force on a charged particle moving in a magnetic field is indeed a vector quantity.
- It is derived from the cross product of the velocity vector and the magnetic field vector.
- Hence, this statement correctly identifies a vector and vector process.
Statement III: Scalar and Scalar - Power
- Power is defined as the rate at which work is done or energy is transferred.
- It can be computed as the dot product of force (vector) and velocity (vector), resulting in a scalar quantity.
- Hence, this statement accurately identifies a scalar product.
Conclusion
Based on the analysis:
- I is incorrect.
- II is correct (Vector and Vector: Magnetic Force).
- III is also correct (Scalar and Scalar: Power).
Thus, the correct answer is option 'C' (II and III).
|
Explore Courses for MCAT exam
|
|
Top Courses for MCATView all
Question Description
Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer? for MCAT 2025 is part of MCAT preparation. The Question and answers have been prepared according to the MCAT exam syllabus. Information about Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for MCAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer?.
Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer? for MCAT 2025 is part of MCAT preparation. The Question and answers have been prepared according to the MCAT exam syllabus. Information about Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for MCAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for MCAT.
Download more important topics, notes, lectures and mock test series for MCAT Exam by signing up for free.
Here you can find the meaning of Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following statements correctly identifies an example of the respective scalar or vector product processes?I. Vector and scalar : torqueII. Vector and vector : magnetic forceIII. Scalar and scalar : powera)I and IIb)III onlyc)II and IIId)I onlyCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice MCAT tests.
|
|
Explore Courses for MCAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily