Electronics and Communication Engineering (ECE) Exam > Electronics and Communication Engineering (ECE) Questions > What is the capacity of an additive white Gau...
Start Learning for Free
What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9) W/Hz?
- a)17.4 Mbit/s
- b)12.28 Mbit/s
- c)26.56 Mbit/s
- d)6.64 Mbit/s
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
What is the capacity of an additive white Gaussian noise channel with ...
Additive white Gaussian noise (AWGN) is a basic noise model used in information theory to mimic the effect of many random processes that occur in nature.
The modifiers denote specific characteristics: Additive because it is added to any noise that might be intrinsic to the information system.
The capacity of an additive white Gaussian noise channel by Shanon's formula:
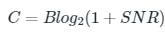
Where B refers to the bandwidth of the channel
SNR means Signal to Noise Ratio : can be defined as the ratio of relevant to irrelevant information in an interface or communication channel.
SNR now can be calculated as,
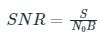
In the above problem, S is the signal power which is equivalent to 10 W.
Bandwidth = 1 MHz
Noise power spectral density of No/2 = 10(−9) W/Hz
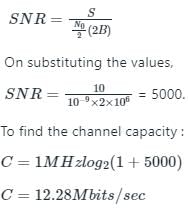
The modifiers denote specific characteristics: Additive because it is added to any noise that might be intrinsic to the information system.
The capacity of an additive white Gaussian noise channel by Shanon's formula:
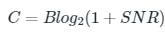
Where B refers to the bandwidth of the channel
SNR means Signal to Noise Ratio : can be defined as the ratio of relevant to irrelevant information in an interface or communication channel.
SNR now can be calculated as,
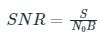
In the above problem, S is the signal power which is equivalent to 10 W.
Bandwidth = 1 MHz
Noise power spectral density of No/2 = 10(−9) W/Hz
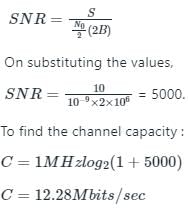
Most Upvoted Answer
What is the capacity of an additive white Gaussian noise channel with ...
The capacity of an additive white Gaussian noise (AWGN) channel can be calculated using the formula:
C = B * log2(1 + SNR)
where C is the capacity in bits per second, B is the bandwidth in Hz, and SNR is the signal-to-noise ratio.
In this case, the bandwidth is given as 1 MHz, which is equal to 1,000,000 Hz. The power is given as 10W, and the noise power spectral density is given as No/2 = 10(-10).
The signal-to-noise ratio (SNR) can be calculated as:
SNR = (signal power) / (noise power)
The signal power can be calculated using the formula:
signal power = power * bandwidth
In this case, the signal power is:
signal power = 10W * 1,000,000 Hz = 10^7 W*Hz
The noise power can be calculated as:
noise power = noise power spectral density * bandwidth
In this case, the noise power is:
noise power = 10(-10) * 1,000,000 Hz = 10^(-3) W*Hz
Now, we can calculate the SNR:
SNR = (signal power) / (noise power)
= (10^7) / (10^(-3))
= 10^10
Finally, we can calculate the capacity:
C = B * log2(1 + SNR)
= 1,000,000 Hz * log2(1 + 10^10)
≈ 23.25 Mbps
Therefore, the capacity of the AWGN channel is approximately 23.25 Mbps.
C = B * log2(1 + SNR)
where C is the capacity in bits per second, B is the bandwidth in Hz, and SNR is the signal-to-noise ratio.
In this case, the bandwidth is given as 1 MHz, which is equal to 1,000,000 Hz. The power is given as 10W, and the noise power spectral density is given as No/2 = 10(-10).
The signal-to-noise ratio (SNR) can be calculated as:
SNR = (signal power) / (noise power)
The signal power can be calculated using the formula:
signal power = power * bandwidth
In this case, the signal power is:
signal power = 10W * 1,000,000 Hz = 10^7 W*Hz
The noise power can be calculated as:
noise power = noise power spectral density * bandwidth
In this case, the noise power is:
noise power = 10(-10) * 1,000,000 Hz = 10^(-3) W*Hz
Now, we can calculate the SNR:
SNR = (signal power) / (noise power)
= (10^7) / (10^(-3))
= 10^10
Finally, we can calculate the capacity:
C = B * log2(1 + SNR)
= 1,000,000 Hz * log2(1 + 10^10)
≈ 23.25 Mbps
Therefore, the capacity of the AWGN channel is approximately 23.25 Mbps.
|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|
|
Top Courses for Electronics and Communication Engineering (ECE)View all
Question Description
What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2025 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer?.
What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer? for Electronics and Communication Engineering (ECE) 2025 is part of Electronics and Communication Engineering (ECE) preparation. The Question and answers have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. Information about What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer?.
Solutions for What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electronics and Communication Engineering (ECE).
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Here you can find the meaning of What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9)W/Hz?a)17.4 Mbit/sb)12.28 Mbit/sc)26.56 Mbit/sd)6.64 Mbit/sCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Electronics and Communication Engineering (ECE) tests.
|
|
Explore Courses for Electronics and Communication Engineering (ECE) exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
x
![]()
Best way to Prepare for Electronics and Communication Engineering (ECE)
Learn | Test | Discuss | Repeat
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup