UGC NET Exam > UGC NET Questions > A particle in 1-D moves under the influence o...
Start Learning for Free
A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For large n the quantized energy En depends on n as:
- a)E∝n4/3
- b)E∝n3/4
- c)E∝n2/3
- d)E∝n3/2
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
A particle in 1-D moves under the influence of a potential of V(x) a x...
Concept:
According to WKB approximation:
We have to use the relation that:

where, β1=β2=π/4, for V (x) to be finite a boundary and β1=β2=0 , for V(x) to be infinite at the boundary.
Explanation:
We have a particle in 1-D that moves under the influence of a potential of V(x) a x4.
We use the above formula with β1=β2= π/4 as the potential is finite at the turning points, and we get:
The potential is symmetric hence,
 where A is some constant
where A is some constant
Taking the substitution we get:
we get:
Now pulling out all the E terms, out and doing the integration we get:
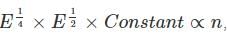 This constant carries a constant after doing the integration.
This constant carries a constant after doing the integration.
Now solving it a bit we get:
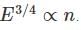
According to WKB approximation:
We have to use the relation that:

where, β1=β2=π/4, for V (x) to be finite a boundary and β1=β2=0 , for V(x) to be infinite at the boundary.
Explanation:
We have a particle in 1-D that moves under the influence of a potential of V(x) a x4.
We use the above formula with β1=β2= π/4 as the potential is finite at the turning points, and we get:
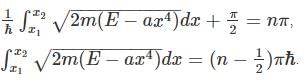
The potential is symmetric hence,
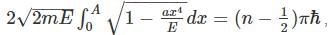 where A is some constant
where A is some constantTaking the substitution
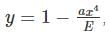 we get:
we get: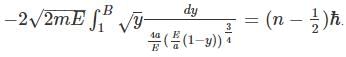
Now pulling out all the E terms, out and doing the integration we get:
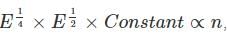 This constant carries a constant after doing the integration.
This constant carries a constant after doing the integration.Now solving it a bit we get:
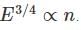
Most Upvoted Answer
A particle in 1-D moves under the influence of a potential of V(x) a x...
The quantized energy levels for a particle in a 1-dimensional potential can be found by solving the time-independent Schrödinger equation:
[-(h_bar^2/2m) * d^2/dx^2 + V(x)] ψ(x) = E ψ(x)
Given that the potential is V(x) = a x^4, we can substitute this into the Schrödinger equation:
[-(h_bar^2/2m) * d^2/dx^2 + a x^4] ψ(x) = E ψ(x)
To simplify the equation, we can make a change of variables by defining y = x^2. This allows us to rewrite the equation as:
[-(h_bar^2/2m) * (1/4) d^2/dy^2 + a y^2] ψ(y) = E ψ(y)
Now, let's solve this equation. The general solution for ψ(y) can be written as:
ψ(y) = C e^(-α y^2) y^β
where α and β are constants to be determined, and C is a normalization constant.
Plugging this solution into the Schrödinger equation, we get:
[-(h_bar^2/2m) * (1/4) (2β(2β - 1) y^(2β - 2) - 4α y^2) + a y^2] C e^(-α y^2) y^β = E C e^(-α y^2) y^β
Simplifying, we find:
[-(h_bar^2/2m) * β(2β - 1) + a] y^(2β) e^(-α y^2) = E y^(2β) e^(-α y^2)
Since y = x^2, this equation can be rewritten as:
[-(h_bar^2/2m) * β(2β - 1) + a] x^(4β) e^(-α x^2) = E x^(4β) e^(-α x^2)
Dividing both sides by x^(4β) e^(-α x^2), we get:
[-(h_bar^2/2m) * β(2β - 1) + a] = E
This equation determines the quantized energy levels E in terms of the constant a and the parameter β. The value of β can be determined by considering the boundary conditions of the system. Without further information about the system, it is not possible to determine the precise dependence of E on a.
[-(h_bar^2/2m) * d^2/dx^2 + V(x)] ψ(x) = E ψ(x)
Given that the potential is V(x) = a x^4, we can substitute this into the Schrödinger equation:
[-(h_bar^2/2m) * d^2/dx^2 + a x^4] ψ(x) = E ψ(x)
To simplify the equation, we can make a change of variables by defining y = x^2. This allows us to rewrite the equation as:
[-(h_bar^2/2m) * (1/4) d^2/dy^2 + a y^2] ψ(y) = E ψ(y)
Now, let's solve this equation. The general solution for ψ(y) can be written as:
ψ(y) = C e^(-α y^2) y^β
where α and β are constants to be determined, and C is a normalization constant.
Plugging this solution into the Schrödinger equation, we get:
[-(h_bar^2/2m) * (1/4) (2β(2β - 1) y^(2β - 2) - 4α y^2) + a y^2] C e^(-α y^2) y^β = E C e^(-α y^2) y^β
Simplifying, we find:
[-(h_bar^2/2m) * β(2β - 1) + a] y^(2β) e^(-α y^2) = E y^(2β) e^(-α y^2)
Since y = x^2, this equation can be rewritten as:
[-(h_bar^2/2m) * β(2β - 1) + a] x^(4β) e^(-α x^2) = E x^(4β) e^(-α x^2)
Dividing both sides by x^(4β) e^(-α x^2), we get:
[-(h_bar^2/2m) * β(2β - 1) + a] = E
This equation determines the quantized energy levels E in terms of the constant a and the parameter β. The value of β can be determined by considering the boundary conditions of the system. Without further information about the system, it is not possible to determine the precise dependence of E on a.

|
Explore Courses for UGC NET exam
|

|
Similar UGC NET Doubts
A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer?
Question Description
A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer? for UGC NET 2025 is part of UGC NET preparation. The Question and answers have been prepared according to the UGC NET exam syllabus. Information about A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for UGC NET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer?.
A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer? for UGC NET 2025 is part of UGC NET preparation. The Question and answers have been prepared according to the UGC NET exam syllabus. Information about A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for UGC NET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer?.
Solutions for A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for UGC NET.
Download more important topics, notes, lectures and mock test series for UGC NET Exam by signing up for free.
Here you can find the meaning of A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer?, a detailed solution for A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A particle in 1-D moves under the influence of a potential of V(x) a x4, where a is a real constant. For largenthe quantized energy Endepends onnas:a)E∝n4/3b)E∝n3/4c)E∝n2/3d)E∝n3/2Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice UGC NET tests.

|
Explore Courses for UGC NET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


























