UGC NET Exam > UGC NET Questions > The energy required to create a lattice vacan...
Start Learning for Free
The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximately
- a)exp(-30)
- b)exp(-15)
- c)exp(15)
- d)exp(30)
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
The energy required to create a lattice vacancy in a crystal is equal ...
The equation for number density of vacancies,
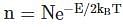 where E : Energy required to form vacancies, N: density of lattice sites.
where E : Energy required to form vacancies, N: density of lattice sites.
Now taking the ratio we get:
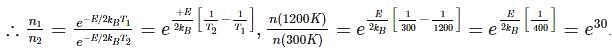
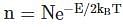 where E : Energy required to form vacancies, N: density of lattice sites.
where E : Energy required to form vacancies, N: density of lattice sites.Now taking the ratio we get:
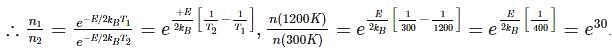
Most Upvoted Answer
The energy required to create a lattice vacancy in a crystal is equal ...
To understand why the correct answer is option 'D', let's analyze the concept of lattice vacancies and their relation to temperature.
Introduction to Lattice Vacancies:
In a crystal lattice, vacancies are the empty spaces where an atom is missing. These vacancies can occur due to various reasons such as thermal fluctuations or crystal defects. The creation of a lattice vacancy requires an input of energy, known as the vacancy formation energy.
Given Information:
According to the question, the energy required to create a lattice vacancy in the crystal is 1 eV. Additionally, we are provided with the temperatures at which the crystal is at equilibrium, 1200 K and 300 K.
Equilibrium at 300 K:
At equilibrium, the number of vacancies created is balanced by the number of vacancies annihilated. At 300 K, the crystal is at a lower temperature, which implies that the thermal energy available is less. Therefore, the number of vacancies created is comparatively smaller.
Calculating the Ratio of Number Densities:
To calculate the ratio of number densities of vacancies at 1200 K and 300 K, we need to consider the Boltzmann distribution. According to this distribution, the probability of finding an atom in a particular energy state is given by the exponential of the negative energy divided by the product of Boltzmann's constant and the temperature.
Let's denote the ratio of number densities as n(1200 K)/n(300 K). Using the Boltzmann distribution, we have:
n(1200 K)/n(300 K) = exp[(E_vacancy)/(k*T_1200)] / exp[(E_vacancy)/(k*T_300)]
where:
- E_vacancy is the vacancy formation energy (1 eV)
- k is Boltzmann's constant (8.617333262145 x 10^-5 eV/K)
- T_1200 is the temperature at 1200 K
- T_300 is the temperature at 300 K
Simplifying the Equation:
Substituting the given values into the equation, we get:
n(1200 K)/n(300 K) = exp[(1 eV)/(8.617333262145 x 10^-5 eV/K * 1200 K)] / exp[(1 eV)/(8.617333262145 x 10^-5 eV/K * 300 K)]
n(1200 K)/n(300 K) = exp[1/(8.617333262145 x 10^-5 * 1200)] / exp[1/(8.617333262145 x 10^-5 * 300)]
n(1200 K)/n(300 K) = exp(1/103.408) / exp(1/25.808)
n(1200 K)/n(300 K) ≈ exp(0.00967) / exp(0.03876)
n(1200 K)/n(300 K) ≈ 1.00972 / 1.0395
n(1200 K)/n(300 K) ≈ 0.9703
Approximating the Result:
The ratio of number densities is approximately 0.9703. Since the value is less than 1, it means that at 1200 K, there are fewer vacancies compared to 300 K.
Converting the Ratio to Exponential Form:
To convert the ratio
Introduction to Lattice Vacancies:
In a crystal lattice, vacancies are the empty spaces where an atom is missing. These vacancies can occur due to various reasons such as thermal fluctuations or crystal defects. The creation of a lattice vacancy requires an input of energy, known as the vacancy formation energy.
Given Information:
According to the question, the energy required to create a lattice vacancy in the crystal is 1 eV. Additionally, we are provided with the temperatures at which the crystal is at equilibrium, 1200 K and 300 K.
Equilibrium at 300 K:
At equilibrium, the number of vacancies created is balanced by the number of vacancies annihilated. At 300 K, the crystal is at a lower temperature, which implies that the thermal energy available is less. Therefore, the number of vacancies created is comparatively smaller.
Calculating the Ratio of Number Densities:
To calculate the ratio of number densities of vacancies at 1200 K and 300 K, we need to consider the Boltzmann distribution. According to this distribution, the probability of finding an atom in a particular energy state is given by the exponential of the negative energy divided by the product of Boltzmann's constant and the temperature.
Let's denote the ratio of number densities as n(1200 K)/n(300 K). Using the Boltzmann distribution, we have:
n(1200 K)/n(300 K) = exp[(E_vacancy)/(k*T_1200)] / exp[(E_vacancy)/(k*T_300)]
where:
- E_vacancy is the vacancy formation energy (1 eV)
- k is Boltzmann's constant (8.617333262145 x 10^-5 eV/K)
- T_1200 is the temperature at 1200 K
- T_300 is the temperature at 300 K
Simplifying the Equation:
Substituting the given values into the equation, we get:
n(1200 K)/n(300 K) = exp[(1 eV)/(8.617333262145 x 10^-5 eV/K * 1200 K)] / exp[(1 eV)/(8.617333262145 x 10^-5 eV/K * 300 K)]
n(1200 K)/n(300 K) = exp[1/(8.617333262145 x 10^-5 * 1200)] / exp[1/(8.617333262145 x 10^-5 * 300)]
n(1200 K)/n(300 K) = exp(1/103.408) / exp(1/25.808)
n(1200 K)/n(300 K) ≈ exp(0.00967) / exp(0.03876)
n(1200 K)/n(300 K) ≈ 1.00972 / 1.0395
n(1200 K)/n(300 K) ≈ 0.9703
Approximating the Result:
The ratio of number densities is approximately 0.9703. Since the value is less than 1, it means that at 1200 K, there are fewer vacancies compared to 300 K.
Converting the Ratio to Exponential Form:
To convert the ratio

|
Explore Courses for UGC NET exam
|

|
Similar UGC NET Doubts
The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer?
Question Description
The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer? for UGC NET 2025 is part of UGC NET preparation. The Question and answers have been prepared according to the UGC NET exam syllabus. Information about The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for UGC NET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer?.
The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer? for UGC NET 2025 is part of UGC NET preparation. The Question and answers have been prepared according to the UGC NET exam syllabus. Information about The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for UGC NET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer?.
Solutions for The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for UGC NET.
Download more important topics, notes, lectures and mock test series for UGC NET Exam by signing up for free.
Here you can find the meaning of The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer?, a detailed solution for The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The energy required to create a lattice vacancy in a crystal is equal to 1 eV. The ratio of the number densities of vacancies n(1200 K)/n(300 K) when the crystal is at equilibrium at 1200 K and 300 K, respectively, is approximatelya)exp(-30)b)exp(-15)c)exp(15)d)exp(30)Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice UGC NET tests.

|
Explore Courses for UGC NET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























