Every day a widget supplier supplies widgets from the warehouse (W) to four locations andndash; Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer?

EduRev

All Courses

Explore Courses UPSC Exam UPSC Test Series Free Notes EduRev Infinity

Open App

CAT Exam > CAT Questions > Every day a widget supplier supplies widgets ...

Join the Discussion on the App

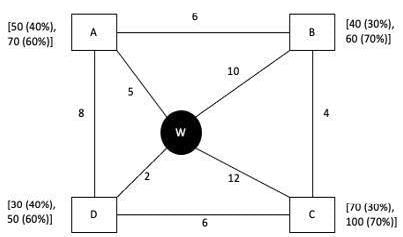
Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.

Q. If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?

a)
18%
b)
5.4%
c)
30%
d)
3.24%

Correct answer is option 'A'. Can you explain this answer?

FREE This question is part of

CAT 2022 Slot 2: Past Year Question Paper

Attempt Test

Attempt this Test

View all answers Start learning for free

< Previous Question Next Question >

Explore Courses for CAT exam

Similar CAT Doubts

Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (

View answer

Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (

View answer

Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (

View answer

Directions: The passage given below is followed by a set of four questions. Choose the best answer to each question.The treatment of probability has been confused by mathematicians. From the beginning there was an ambiguity in dealing with the calculus of probability. When the Cehvalier de Mere consulted Pascal on the problems involved in the games of dice, the great mathematician should have frankly told his friend the truth, namely, that mathematics could not be of any use to the gambler in a game of pure chance. Instead he wrapped his answer in the symbolic language of mathematics. What could easily be explained in a few sentences of mundane speech was expressed in a terminology which was unfamiliar to the immense majority and therefore regarded with reverential awe. People suspected that the puzzling formulae contain some important revelations, hidden to the uninitiated; they got the impression that a scientific method of gambling exists and that the esoteric teachings of mathematics provide a key to winning. The heavenly mystic Pascal unintentionally became the patron saint of gambling. The textbooks of the calculus of probability gratuitously propagandize for the gambling casinos precisely because they are sealed books to the layman.There are two entirely different instances of probability; we may call them class probability (or frequency probability) and case probability (or the specific understanding of the sciences of human action). The field for the application of the former is the field of the natural sciences, entirely ruled by causality; the field for the application of the latter is the field of the sciences of human action, entirely ruled by teleology.Class probability means: We know or assume to know, with regard to the problem concerned, everything about the behavior of a whole class of events or phenomena; but about the actual singular events or phenomena we know nothing but that they are elements of this class. We know, for instance, that there are ninety tickets in a lottery and that five of them will be drawn. Thus we know all about the behavior of the whole class of tickets. But with regard to the singular tickets we do not know anything but that they arc elements of this class of ticketsCase probability means: We know, with regard to a particular event, some of the factors which determine its outcome; but there are other determining factors about which we know nothing. Case probability has nothing in common with class probability but the incompleteness of our knowledge. In every other regard the two are entirely differentThere are, of course, many instances in which men try to forecast a particular future event on the basis of their knowledge about the behavior of the class. A doctor may determine the chances for the full recovery of his patient if he knows that 70 per cent of those afflicted with the same disease recover. If he expresses his judgment correctly, he will not say more than that the probability of recovery is 0.7, that is, out of ten patients not more than three on the average die. All such predictions about external events, i.e., events in the field of the natural sciences, are of this character. They are in fact not forecasts about the issue of the case in question, but statements about the frequency of the various possible outcomes. They arc based either on statistical information or simply on the rough estimate of the frequency derived from nonstatistical experience.As far as such types of probable statements are concerned, we are not faced with case probability. In fact we do not know anything about the case in question except that it is an instance of a class the behavior of which we know or think we know.A surgeon tells a patient who considers submitting himself to an operation that thirty out of every hundred undergoing such an operation die. If the patient asks whether this number of deaths is already full, he has misunderstood the sense of the doctor's statement. He has fallen prey to the error known as the "gambler's fallacy." Like the roulette player who concludes from a run often red in succession that the probability of the next turn being black is now greater than it was before the run, he confuses case probability with class probability.Which of the following is an example of case probability?

View answer

Directions: The passage given below is followed by a set of four questions. Choose the best answer to each question.The treatment of probability has been confused by mathematicians. From the beginning there was an ambiguity in dealing with the calculus of probability. When the Cehvalier de Mere consulted Pascal on the problems involved in the games of dice, the great mathematician should have frankly told his friend the truth, namely, that mathematics could not be of any use to the gambler in a game of pure chance. Instead he wrapped his answer in the symbolic language of mathematics. What could easily be explained in a few sentences of mundane speech was expressed in a terminology which was unfamiliar to the immense majority and therefore regarded with reverential awe. People suspected that the puzzling formulae contain some important revelations, hidden to the uninitiated; they got the impression that a scientific method of gambling exists and that the esoteric teachings of mathematics provide a key to winning. The heavenly mystic Pascal unintentionally became the patron saint of gambling. The textbooks of the calculus of probability gratuitously propagandize for the gambling casinos precisely because they are sealed books to the layman.There are two entirely different instances of probability; we may call them class probability (or frequency probability) and case probability (or the specific understanding of the sciences of human action). The field for the application of the former is the field of the natural sciences, entirely ruled by causality; the field for the application of the latter is the field of the sciences of human action, entirely ruled by teleology.Class probability means: We know or assume to know, with regard to the problem concerned, everything about the behavior of a whole class of events or phenomena; but about the actual singular events or phenomena we know nothing but that they are elements of this class. We know, for instance, that there are ninety tickets in a lottery and that five of them will be drawn. Thus we know all about the behavior of the whole class of tickets. But with regard to the singular tickets we do not know anything but that they arc elements of this class of ticketsCase probability means: We know, with regard to a particular event, some of the factors which determine its outcome; but there are other determining factors about which we know nothing. Case probability has nothing in common with class probability but the incompleteness of our knowledge. In every other regard the two are entirely differentThere are, of course, many instances in which men try to forecast a particular future event on the basis of their knowledge about the behavior of the class. A doctor may determine the chances for the full recovery of his patient if he knows that 70 per cent of those afflicted with the same disease recover. If he expresses his judgment correctly, he will not say more than that the probability of recovery is 0.7, that is, out of ten patients not more than three on the average die. All such predictions about external events, i.e., events in the field of the natural sciences, are of this character. They are in fact not forecasts about the issue of the case in question, but statements about the frequency of the various possible outcomes. They arc based either on statistical information or simply on the rough estimate of the frequency derived from nonstatistical experience.As far as such types of probable statements are concerned, we are not faced with case probability. In fact we do not know anything about the case in question except that it is an instance of a class the behavior of which we know or think we know.A surgeon tells a patient who considers submitting himself to an operation that thirty out of every hundred undergoing such an operation die. If the patient asks whether this number of deaths is already full, he has misunderstood the sense of the doctor's statement. He has fallen prey to the error known as the "gambler's fallacy." Like the roulette player who concludes from a run often red in succession that the probability of the next turn being black is now greater than it was before the run, he confuses case probability with class probability.Which of the following is not true about case probability and class probability?

View answer

Top Courses for CATView all

Quantitative Aptitude (Quant)

Crash Course for CAT

CAT Mock Test Series 2024

Mock Test Series for SNAP

Mock Test Series for XAT

Top Courses for CAT

View all

Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer?

Share with a Friend

Answer this doubt

Question Description
Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer? for CAT 2024 is part of CAT preparation. The Question and answers have been prepared according to the CAT exam syllabus. Information about Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for CAT 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer?.

Solutions for Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for CAT. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free.

Here you can find the meaning of Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer?, a detailed solution for Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an ample number of questions to practice Every day a widget supplier supplies widgets from the warehouse (W) to four locations – Ahmednagar (A), Bikrampore (B), Chitrachak (C), and Deccan Park (D). The daily demand for widgets in each location is uncertain and independent of each other. Demands andcorresponding probability values (in parenthesis) are given against each location (A, B, C, and D) in the figure below. For example, there is a 40% chance that the demand in Ahmednagar will be 50 units and a 60% chance that the demand will be 70 units. The lines in the figure connecting the locations and warehouse represent two-way roads connecting those places with the distances (in km) shown beside the line. The distances in both the directions along a road are equal. For example, the road from Ahmednagar to Bikrampore and the road from Bikrampore to Ahmednagar are both 6 km long.Every day the supplier gets the information about the demand values of the four locations and creates the travel route that starts from the warehouse and ends at a location after visiting all the locations exactly once. While making the route plan, the supplier goes to the locations in decreasing order of demand. If there is a tie for the choice of the next location, the supplier will go to the location closest to the current location. Also, while creating the route, the supplier can either follow the direct path (if available) from one location to another or can take the path via the warehouse. If both paths are available (direct and via warehouse), the supplier will choose the path with minimum distance.Q.If the first location visited from the warehouse is Ahmednagar, then what is the chance that the total distance covered in the route is 40 km?a)18%b)5.4%c)30%d)3.24%Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice CAT tests.

Explore Courses for CAT exam