GMAT Exam > GMAT Questions > y = x2+ bx + 256 cuts the x axis at (h, 0) an...
Start Learning for Free
y = x2 + bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?
- a)-32
- b)-256
- c)-255
- d)-257
- e)0
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are ...
Step 1: Understand the equation and the points (h, 0) and (k, 0)
The given equation is a quadratic equation. A quadratic equation when plotted on a graph sheet (x - y plane) will result in a parabola.
The roots of the quadratic equation are computed by equating the quadratic expression to 0. i.e., the roots are the values that 'x' take when y = 0
So, the roots of the quadratic equation are the points where the parabola cuts the x-axis.
The question mentions that the curve described by the equation cuts the x-axis at (h, 0) and (k, 0). So, h and k are the roots of the quadratic equation.
For quadratic equations of the form ax2 + bx + c = 0, the sum of the roots =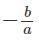
The sum of the roots of this equation is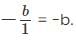
Note : Higher the value of 'b', i.e., higher the sum of the roots of this quadratic equation, lower the value of b.
The roots of the quadratic equation are computed by equating the quadratic expression to 0. i.e., the roots are the values that 'x' take when y = 0
So, the roots of the quadratic equation are the points where the parabola cuts the x-axis.
The question mentions that the curve described by the equation cuts the x-axis at (h, 0) and (k, 0). So, h and k are the roots of the quadratic equation.
For quadratic equations of the form ax2 + bx + c = 0, the sum of the roots =
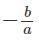
The sum of the roots of this equation is
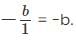
Note : Higher the value of 'b', i.e., higher the sum of the roots of this quadratic equation, lower the value of b.
For quadratic equations of the form ax2 + bx + c = 0, the product of roots = c/a.
Therefore, the product of the roots of this equation = 256/1 = 256.
i.e., h × k = 256 h and k are both integers.
So, h and k are both integral factors of 256.
Therefore, the product of the roots of this equation = 256/1 = 256.
i.e., h × k = 256 h and k are both integers.
So, h and k are both integral factors of 256.
Step 2: List possible values of h and k and find the least value of ‘b’
This is the step in which number properties concepts kick in. 256 can be expressed as product of two numbers in the following ways:
1 × 256
2 × 128
4 × 64
8 × 32
16 × 16
1 × 256
2 × 128
4 × 64
8 × 32
16 × 16
The sum of the roots is maximum when the roots are 1 and 256 and the maximum sum is 1 + 256 = 257.
∴ The least value possible for b is -257.
∴ The least value possible for b is -257.
Choice D is the correct answer.
Most Upvoted Answer
y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are ...
Understanding the Problem
The quadratic equation given is:
y = x² + bx + 256
This equation intersects the x-axis at points (h, 0) and (k, 0). Here, h and k are the roots of the equation.
Using Vieta's Formulas
According to Vieta’s formulas:
- The sum of the roots (h + k) = -b
- The product of the roots (h * k) = 256
Finding Integer Roots
We need to explore integer pairs (h, k) that satisfy the product condition:
h * k = 256
The integer factor pairs of 256 are:
- (1, 256)
- (2, 128)
- (4, 64)
- (8, 32)
- (16, 16)
- (-1, -256)
- (-2, -128)
- (-4, -64)
- (-8, -32)
- (-16, -16)
Calculating b for Each Pair
For each pair (h, k), we can calculate b using the formula:
b = -(h + k)
Now, let's evaluate the pairs:
- (1, 256) → b = -(1 + 256) = -257
- (2, 128) → b = -(2 + 128) = -130
- (4, 64) → b = -(4 + 64) = -68
- (8, 32) → b = -(8 + 32) = -40
- (16, 16) → b = -(16 + 16) = -32
- (-1, -256) → b = -(-1 - 256) = 257
- (-2, -128) → b = -(-2 - 128) = 130
- (-4, -64) → b = -(-4 - 64) = 68
- (-8, -32) → b = -(-8 - 32) = 40
- (-16, -16) → b = -(-16 - 16) = 32
Finding the Least Value of b
From these calculations, the least value of b occurs with the pair (1, 256) or (2, 128).
The minimum b value is:
-257
Thus, the correct answer is option 'D': -257.
The quadratic equation given is:
y = x² + bx + 256
This equation intersects the x-axis at points (h, 0) and (k, 0). Here, h and k are the roots of the equation.
Using Vieta's Formulas
According to Vieta’s formulas:
- The sum of the roots (h + k) = -b
- The product of the roots (h * k) = 256
Finding Integer Roots
We need to explore integer pairs (h, k) that satisfy the product condition:
h * k = 256
The integer factor pairs of 256 are:
- (1, 256)
- (2, 128)
- (4, 64)
- (8, 32)
- (16, 16)
- (-1, -256)
- (-2, -128)
- (-4, -64)
- (-8, -32)
- (-16, -16)
Calculating b for Each Pair
For each pair (h, k), we can calculate b using the formula:
b = -(h + k)
Now, let's evaluate the pairs:
- (1, 256) → b = -(1 + 256) = -257
- (2, 128) → b = -(2 + 128) = -130
- (4, 64) → b = -(4 + 64) = -68
- (8, 32) → b = -(8 + 32) = -40
- (16, 16) → b = -(16 + 16) = -32
- (-1, -256) → b = -(-1 - 256) = 257
- (-2, -128) → b = -(-2 - 128) = 130
- (-4, -64) → b = -(-4 - 64) = 68
- (-8, -32) → b = -(-8 - 32) = 40
- (-16, -16) → b = -(-16 - 16) = 32
Finding the Least Value of b
From these calculations, the least value of b occurs with the pair (1, 256) or (2, 128).
The minimum b value is:
-257
Thus, the correct answer is option 'D': -257.
|
Explore Courses for GMAT exam
|
|
Top Courses for GMATView all
Question Description
y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer?.
y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer? for GMAT 2025 is part of GMAT preparation. The Question and answers have been prepared according to the GMAT exam syllabus. Information about y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GMAT 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer?.
Solutions for y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for GMAT.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Here you can find the meaning of y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer?, a detailed solution for y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice y = x2+ bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?a)-32b)-256c)-255d)-257e)0Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice GMAT tests.
|
|
Explore Courses for GMAT exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup