Civil Engineering (CE) Exam > Civil Engineering (CE) Questions > Which one of the following is of greater sign...
Start Learning for Free
Which one of the following is of greater significance in representing strength of section of a beam?
- a)Section modulus
- b)Poisson's ratio
- c)Elasticity constant
- d)Coefficient of linear expansion
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
Which one of the following is of greater significance in representing ...
Strength of section of a beam depends upon section modulus (Z).
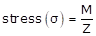
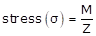
Most Upvoted Answer
Which one of the following is of greater significance in representing ...
Section Modulus:
The section modulus of a beam is a geometric property that represents the strength of a particular section of the beam. It is defined as the ratio of moment of inertia of the section to the distance from the neutral axis, which is a measure of the resistance to bending. In simple terms, it indicates how far away the outer fibers of a section are located from the neutral axis, and a greater section modulus implies a greater resistance to bending.
Poisson's Ratio:
Poisson's ratio is a material property that represents the ratio of lateral strain to longitudinal strain under an applied stress. It measures the degree of deformation in the transverse direction when a material is subjected to a longitudinal stress. Poisson's ratio is not directly related to the strength of a section of a beam but rather describes the material's ability to deform elastically under stress.
Elasticity Constant:
Elasticity constant, also known as Young's modulus or modulus of elasticity, is a material property that represents the ratio of stress to strain within the elastic range. It quantifies the stiffness of a material and describes how much it deforms under an applied force. Similar to Poisson's ratio, elasticity constant is not directly related to the strength of a section of a beam, but rather characterizes the material's response to stress.
Coefficient of Linear Expansion:
The coefficient of linear expansion is a material property that represents the change in length of a material per unit length for a one-degree change in temperature. It describes how a material expands or contracts when subjected to temperature variations. The coefficient of linear expansion is not directly related to the strength of a section of a beam but rather describes the material's thermal behavior.
Significance of Section Modulus:
The section modulus is of greater significance in representing the strength of a section of a beam compared to the other options. Here's why:
1. Bending Resistance: The section modulus directly relates to the resistance of a section to bending. A larger section modulus indicates that the outer fibers of the section are located farther away from the neutral axis, resulting in a greater resistance to bending.
2. Structural Design: Engineers use the section modulus to design beams that can withstand bending moments and prevent failure. By considering the section modulus, they can select the appropriate beam dimensions and material properties to ensure structural integrity.
3. Efficiency and Economy: By optimizing the section modulus, engineers can design beams that are efficient and economical. By selecting a section with an optimal section modulus, they can minimize the amount of material used while still meeting the required strength criteria.
4. Flexural Strength: The section modulus is directly related to the flexural strength of a beam. A higher section modulus implies a greater ability to resist bending stresses, ultimately leading to a higher flexural strength.
In conclusion, the section modulus is of greater significance in representing the strength of a section of a beam compared to Poisson's ratio, elasticity constant, and coefficient of linear expansion. It directly relates to the beam's resistance to bending, is crucial in structural design, contributes to efficiency and economy, and is a key factor in determining the beam's flexural strength.
The section modulus of a beam is a geometric property that represents the strength of a particular section of the beam. It is defined as the ratio of moment of inertia of the section to the distance from the neutral axis, which is a measure of the resistance to bending. In simple terms, it indicates how far away the outer fibers of a section are located from the neutral axis, and a greater section modulus implies a greater resistance to bending.
Poisson's Ratio:
Poisson's ratio is a material property that represents the ratio of lateral strain to longitudinal strain under an applied stress. It measures the degree of deformation in the transverse direction when a material is subjected to a longitudinal stress. Poisson's ratio is not directly related to the strength of a section of a beam but rather describes the material's ability to deform elastically under stress.
Elasticity Constant:
Elasticity constant, also known as Young's modulus or modulus of elasticity, is a material property that represents the ratio of stress to strain within the elastic range. It quantifies the stiffness of a material and describes how much it deforms under an applied force. Similar to Poisson's ratio, elasticity constant is not directly related to the strength of a section of a beam, but rather characterizes the material's response to stress.
Coefficient of Linear Expansion:
The coefficient of linear expansion is a material property that represents the change in length of a material per unit length for a one-degree change in temperature. It describes how a material expands or contracts when subjected to temperature variations. The coefficient of linear expansion is not directly related to the strength of a section of a beam but rather describes the material's thermal behavior.
Significance of Section Modulus:
The section modulus is of greater significance in representing the strength of a section of a beam compared to the other options. Here's why:
1. Bending Resistance: The section modulus directly relates to the resistance of a section to bending. A larger section modulus indicates that the outer fibers of the section are located farther away from the neutral axis, resulting in a greater resistance to bending.
2. Structural Design: Engineers use the section modulus to design beams that can withstand bending moments and prevent failure. By considering the section modulus, they can select the appropriate beam dimensions and material properties to ensure structural integrity.
3. Efficiency and Economy: By optimizing the section modulus, engineers can design beams that are efficient and economical. By selecting a section with an optimal section modulus, they can minimize the amount of material used while still meeting the required strength criteria.
4. Flexural Strength: The section modulus is directly related to the flexural strength of a beam. A higher section modulus implies a greater ability to resist bending stresses, ultimately leading to a higher flexural strength.
In conclusion, the section modulus is of greater significance in representing the strength of a section of a beam compared to Poisson's ratio, elasticity constant, and coefficient of linear expansion. It directly relates to the beam's resistance to bending, is crucial in structural design, contributes to efficiency and economy, and is a key factor in determining the beam's flexural strength.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Question Description
Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer?.
Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer? for Civil Engineering (CE) 2025 is part of Civil Engineering (CE) preparation. The Question and answers have been prepared according to the Civil Engineering (CE) exam syllabus. Information about Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for Civil Engineering (CE).
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Here you can find the meaning of Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which one of the following is of greater significance in representing strength of section of a beam?a)Section modulusb)Poissons ratioc)Elasticity constantd)Coefficient of linear expansionCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice Civil Engineering (CE) tests.

|
Explore Courses for Civil Engineering (CE) exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























