Class 12 Exam > Class 12 Questions > One Integer Value Correct TypeThis section co...
Start Learning for Free
One Integer Value Correct Type
This section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)
This section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)
Q.
Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .
Correct answer is '4'. Can you explain this answer?
Verified Answer
One Integer Value Correct TypeThis section contains 1 question, when w...
Most Upvoted Answer
One Integer Value Correct TypeThis section contains 1 question, when w...
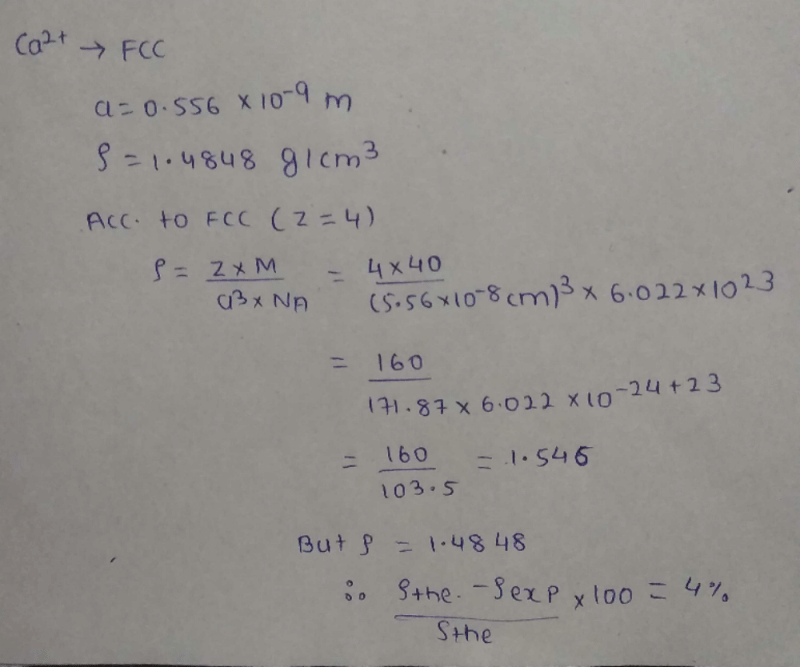
Free Test
FREE
| Start Free Test |
Community Answer
One Integer Value Correct TypeThis section contains 1 question, when w...
Calculation of Schottky Defects in a Face-Centred Cubic Unit Cell
To calculate the percentage of Schottky defects in a face-centred cubic (FCC) unit cell of calcium, we need to first understand what Schottky defects are and how they are related to the crystal structure and density of the material.
Schottky Defects:
- Schottky defects are point defects that occur in ionic crystals.
- They involve the simultaneous absence of an equal number of cations and anions from their lattice sites.
- These defects result in the formation of vacancies in the crystal lattice.
Face-Centred Cubic (FCC) Unit Cell:
- The FCC unit cell is a type of crystal structure where atoms are arranged in a lattice with cubic symmetry.
- In an FCC unit cell, there are atoms at the corners of the cube and one atom at the center of each face of the cube.
- This arrangement gives a total of 4 atoms per unit cell.
Calculation:
1. Calculate the volume of the unit cell:
- The lattice parameter 'a' of the FCC unit cell of calcium is given as 0.556 nm.
- The volume (V) of the unit cell can be calculated using the formula: V = a^3.
- Substituting the given value, V = (0.556 nm)^3.
2. Calculate the mass of the unit cell:
- The density of calcium is given as 1.4848 g/cm^3.
- Since the density is given in g/cm^3, we need to convert the volume from nm^3 to cm^3.
- 1 nm = 10^-7 cm, so (0.556 nm)^3 = (0.556 x 10^-7 cm)^3.
- The mass (m) of the unit cell can be calculated using the formula: m = V x density.
- Substituting the values, m = (0.556 x 10^-7 cm)^3 x 1.4848 g/cm^3.
3. Calculate the number of formula units in the unit cell:
- Since calcium has a face-centered cubic structure, there are 4 atoms per unit cell.
- The number of formula units in the unit cell is equal to the number of atoms divided by the number of atoms per formula unit.
- For calcium, the number of formula units is 4/1 = 4.
4. Calculate the number of Schottky defects:
- Schottky defects involve the absence of an equal number of cations and anions.
- In a unit cell of calcium, there are 4 cations and 4 anions in a perfectly ordered crystal structure.
- The number of Schottky defects can be calculated using the formula: (Number of cations + Number of anions) - Number of formula units.
- Substituting the values, (4 + 4) - 4 = 4.
5. Calculate the percentage of Schottky defects:
- The percentage of Schottky defects is given by the formula: (Number of Schottky defects / Number of formula units) x 100.
- Substituting the values, (4/4) x 100 = 100%.
Conclusion:
The percentage of Schottky defects
To calculate the percentage of Schottky defects in a face-centred cubic (FCC) unit cell of calcium, we need to first understand what Schottky defects are and how they are related to the crystal structure and density of the material.
Schottky Defects:
- Schottky defects are point defects that occur in ionic crystals.
- They involve the simultaneous absence of an equal number of cations and anions from their lattice sites.
- These defects result in the formation of vacancies in the crystal lattice.
Face-Centred Cubic (FCC) Unit Cell:
- The FCC unit cell is a type of crystal structure where atoms are arranged in a lattice with cubic symmetry.
- In an FCC unit cell, there are atoms at the corners of the cube and one atom at the center of each face of the cube.
- This arrangement gives a total of 4 atoms per unit cell.
Calculation:
1. Calculate the volume of the unit cell:
- The lattice parameter 'a' of the FCC unit cell of calcium is given as 0.556 nm.
- The volume (V) of the unit cell can be calculated using the formula: V = a^3.
- Substituting the given value, V = (0.556 nm)^3.
2. Calculate the mass of the unit cell:
- The density of calcium is given as 1.4848 g/cm^3.
- Since the density is given in g/cm^3, we need to convert the volume from nm^3 to cm^3.
- 1 nm = 10^-7 cm, so (0.556 nm)^3 = (0.556 x 10^-7 cm)^3.
- The mass (m) of the unit cell can be calculated using the formula: m = V x density.
- Substituting the values, m = (0.556 x 10^-7 cm)^3 x 1.4848 g/cm^3.
3. Calculate the number of formula units in the unit cell:
- Since calcium has a face-centered cubic structure, there are 4 atoms per unit cell.
- The number of formula units in the unit cell is equal to the number of atoms divided by the number of atoms per formula unit.
- For calcium, the number of formula units is 4/1 = 4.
4. Calculate the number of Schottky defects:
- Schottky defects involve the absence of an equal number of cations and anions.
- In a unit cell of calcium, there are 4 cations and 4 anions in a perfectly ordered crystal structure.
- The number of Schottky defects can be calculated using the formula: (Number of cations + Number of anions) - Number of formula units.
- Substituting the values, (4 + 4) - 4 = 4.
5. Calculate the percentage of Schottky defects:
- The percentage of Schottky defects is given by the formula: (Number of Schottky defects / Number of formula units) x 100.
- Substituting the values, (4/4) x 100 = 100%.
Conclusion:
The percentage of Schottky defects

|
Explore Courses for Class 12 exam
|

|
Similar Class 12 Doubts
One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer?
Question Description
One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer?.
One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer?.
Solutions for One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer?, a detailed solution for One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer? has been provided alongside types of One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice One Integer Value Correct TypeThis section contains 1 question, when worked out will result in an integer value from 0 to 9 (both inclusive)Q.Calcium crystallises in a face-centred cubic unit cell with a = 0.556 nm and density 1.4848 g/cm3. Percentage of Schottky defects in this crystal is ... .Correct answer is '4'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.





















