Class 12 Exam > Class 12 Questions > A ray of light passes through a plane glass s...
Start Learning for Free
A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:
- a)30°
- b)45°
- c)60°
- d)0°
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
A ray of light passes through a plane glass slab of thickness t and re...
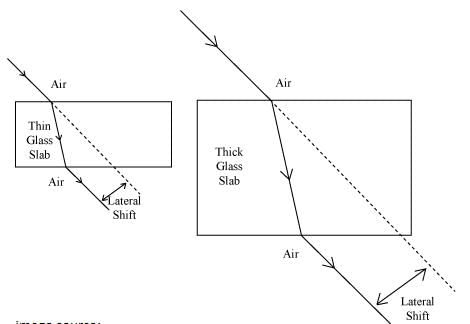
The incident ray and emergent ray are parallel to each other but latteray displaced due to reflaction at two surfaces . So, the angle between them is Zero.
View all questions of this test
Most Upvoted Answer
A ray of light passes through a plane glass slab of thickness t and re...
The incident ray and emergent ray are parallel to each other but latteray displaced due to reflaction at two surfaces . So, the angle between them is Zero.
Free Test
FREE
| Start Free Test |
Community Answer
A ray of light passes through a plane glass slab of thickness t and re...
Explanation:
- When a ray of light passes through a plane glass slab, it undergoes refraction twice.
- First, when it enters the slab from air and second, when it emerges out of the slab into air.
- The refractive index of the glass slab is given as 1.5.
- The angle of incidence (i) and angle of emergence (e) are related to the angle of refraction (r) by Snell's law.
- Snell's law states that n1 sin i = n2 sin r, where n1 and n2 are the refractive indices of the two media and i and r are the angles of incidence and refraction, respectively.
- For the first refraction, the angle of incidence is i and the angle of refraction is r1.
- For the second refraction, the angle of incidence is r2 and the angle of emergence is e.
- Applying Snell's law twice, we get:
- sin i = (1.5) sin r1
- sin r2 = (1/1.5) sin e = (2/3) sin e
- sin i = (2/3) sin e
- Dividing the above two equations, we get:
- sin r1/sin r2 = 3/2
- sin r1 = (3/2) sin r2
- As the angle between the incident ray and emergent ray is the sum of the angles of refraction, we have:
- Angle between incident ray and emergent ray = r1 + r2
- Angle between incident ray and emergent ray = r1 + (sin^-1((2/3)sin i))
- Substituting sin r1 = (3/2) sin r2 in the above equation, we get:
- Angle between incident ray and emergent ray = (3/2) sin r2 + (sin^-1((2/3)sin i))
- Angle between incident ray and emergent ray = (3/2) (sin^-1((2/3)sin e)) + (sin^-1((2/3)sin i))
- As sin^-1((2/3)sin e) and sin^-1((2/3)sin i) are acute angles, their sum is less than or equal to 90 degrees.
- Therefore, the angle between the incident ray and emergent ray is less than or equal to 90 degrees.
- Hence, option 'D' (0 degrees) is the correct answer as the angle between the incident ray and emergent ray is zero degrees, which means they are parallel.

|
Explore Courses for Class 12 exam
|

|
Question Description
A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer?.
A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer? for Class 12 2025 is part of Class 12 preparation. The Question and answers have been prepared according to the Class 12 exam syllabus. Information about A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Class 12 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer?.
Solutions for A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Class 12.
Download more important topics, notes, lectures and mock test series for Class 12 Exam by signing up for free.
Here you can find the meaning of A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer?, a detailed solution for A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A ray of light passes through a plane glass slab of thickness t and refractive index μ = 1.5. The angle between the incident ray and emergent ray will be:a)30°b)45°c)60°d)0°Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Class 12 tests.

|
Explore Courses for Class 12 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























