NEET Exam > NEET Questions > Which of the following statements not true?a)...
Start Learning for Free
Which of the following statements not true?
- a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point
- b)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector
- c)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centre
- d)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centre
Correct answer is option 'D'. Can you explain this answer?
Most Upvoted Answer
Which of the following statements not true?a)The velocity vector of a ...
Understanding Circular Motion and Acceleration
In circular motion, it's crucial to differentiate between uniform and non-uniform circular motion. The statements provided touch on these concepts.
Analysis of Each Statement
- Statement A: The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point.
This statement is true. In circular motion, the velocity is tangential to the circle.
- Statement B: The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
This statement is also true. Over one full cycle, the direction of the acceleration changes but the average vector sums to zero.
- Statement C: The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the center.
This statement is true. In uniform circular motion, the acceleration (centripetal) is directed inward toward the center.
- Statement D: The net acceleration of a particle in circular motion is always along the radius of the circle towards the center.
This statement is false. While centripetal acceleration is always directed towards the center in uniform circular motion, in non-uniform circular motion, tangential acceleration exists, which is not directed towards the center. Therefore, the net acceleration can have components both radial and tangential.
Conclusion
The correct answer is option 'D' as it incorrectly suggests that the net acceleration is always directed towards the center, ignoring the possibility of tangential acceleration in non-uniform circular motion.
In circular motion, it's crucial to differentiate between uniform and non-uniform circular motion. The statements provided touch on these concepts.
Analysis of Each Statement
- Statement A: The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point.
This statement is true. In circular motion, the velocity is tangential to the circle.
- Statement B: The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
This statement is also true. Over one full cycle, the direction of the acceleration changes but the average vector sums to zero.
- Statement C: The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the center.
This statement is true. In uniform circular motion, the acceleration (centripetal) is directed inward toward the center.
- Statement D: The net acceleration of a particle in circular motion is always along the radius of the circle towards the center.
This statement is false. While centripetal acceleration is always directed towards the center in uniform circular motion, in non-uniform circular motion, tangential acceleration exists, which is not directed towards the center. Therefore, the net acceleration can have components both radial and tangential.
Conclusion
The correct answer is option 'D' as it incorrectly suggests that the net acceleration is always directed towards the center, ignoring the possibility of tangential acceleration in non-uniform circular motion.
Free Test
FREE
| Start Free Test |
Community Answer
Which of the following statements not true?a)The velocity vector of a ...
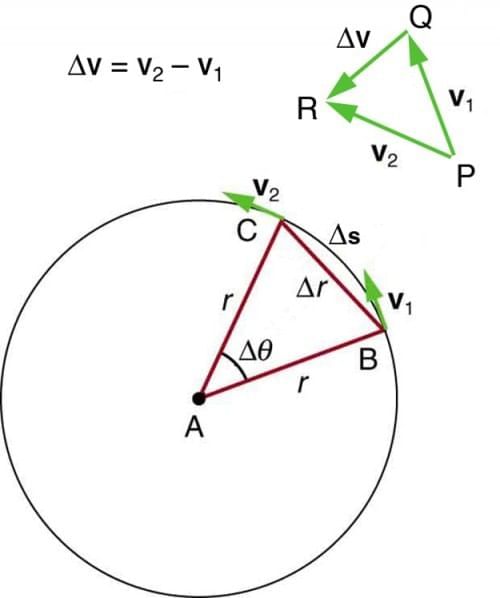
Option A: True. The velocity vector of a particle at any point on its path is always tangent to the path at that point, as velocity represents the direction of motion.
Option B: True. For a particle in uniform circular motion, the centripetal acceleration points towards the center. Over one complete cycle, the acceleration vectors cancel out, resulting in an average acceleration of zero (null vector).
Option C: True. The net acceleration in uniform circular motion is centripetal acceleration, which always points towards the center of the circle along the radius.
Option D: Not true. This statement is incorrect because it implies that the net acceleration in all types of circular motion is always radial. While in uniform circular motion, the acceleration is purely radial, in non-uniform circular motion, there is an additional tangential component of acceleration due to the change in speed. Thus, the net acceleration in such cases is not always directed towards the center.
|
Explore Courses for NEET exam
|
|
Top Courses for NEETView all
Question Description
Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer?.
Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer?.
Solutions for Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following statements not true?a)The velocity vector of a particle at a point is always along the tangent to the path of the particle at that pointb)The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vectorc)The net acceleration of a particle in uniform circular motion is always along the radius of the circle towards the centred)The net acceleration of a particle in circular motion is always along the radius of the circle towards the centreCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice NEET tests.
|
|
Explore Courses for NEET exam
|
|
Signup to solve all Doubts
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup