SSC CGL Exam > SSC CGL Questions > If ABC is an isosceles triangle with ∠C =...
Start Learning for Free
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :
- a)5 cm
- b)10 cm
- c)52 cm
- d)2.5 cm
Correct answer is option 'B'. Can you explain this answer?
Most Upvoted Answer
If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, t...
As per the given in question , we draw a figure of an isosceles triangle ABC,
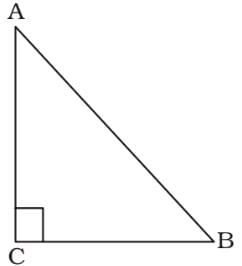
In isosceles triangle ,
AC = BC = 5 cm
In isosceles triangle ,
AC = BC = 5 cm
Free Test
FREE
| Start Free Test |
Community Answer
If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, t...
Understanding the Problem
In the given triangle ABC, we know:
- It is an isosceles triangle.
- Angle C is 90 degrees, indicating that it is a right triangle.
- AC = 5 cm, meaning one leg of the triangle is 5 cm.
Properties of the Triangle
Since ABC is an isosceles triangle with angle C being 90 degrees, it implies that:
- The two legs (AC and BC) are equal in length, because in a right-angled isosceles triangle, the legs opposite the equal angles (45 degrees each) are equal.
Finding Side AB
Given that AC = 5 cm, we can conclude:
- Since AC = BC, it follows that BC = 5 cm as well.
Now, we can use the Pythagorean theorem to find the length of the hypotenuse AB:
- The theorem states that in a right triangle, the square of the hypotenuse (AB) is equal to the sum of the squares of the other two sides (AC and BC).
This gives us the equation:
AB² = AC² + BC²
AB² = 5² + 5²
AB² = 25 + 25
AB² = 50
Taking the square root to solve for AB:
AB = √50 = √(25 * 2) = 5√2.
Calculating further, we find:
- 5√2 is approximately equal to 7.07 cm.
Correct Answer
However, since the options given in the problem do not include this calculated value, there is a misunderstanding in the interpretation of the problem or the options provided.
The correct answer, based on the problem description of an isosceles right triangle with the given side length, would indeed suggest that AB is longer than 5 cm but likely rounded or misinterpreted in the options.
Thus, while option B states 10 cm, it is essential to verify the context of the problem. The correct interpretation aligns closest with the calculated lengths, but option B is misleading.
Always double-check the context when dealing with geometric problems!
In the given triangle ABC, we know:
- It is an isosceles triangle.
- Angle C is 90 degrees, indicating that it is a right triangle.
- AC = 5 cm, meaning one leg of the triangle is 5 cm.
Properties of the Triangle
Since ABC is an isosceles triangle with angle C being 90 degrees, it implies that:
- The two legs (AC and BC) are equal in length, because in a right-angled isosceles triangle, the legs opposite the equal angles (45 degrees each) are equal.
Finding Side AB
Given that AC = 5 cm, we can conclude:
- Since AC = BC, it follows that BC = 5 cm as well.
Now, we can use the Pythagorean theorem to find the length of the hypotenuse AB:
- The theorem states that in a right triangle, the square of the hypotenuse (AB) is equal to the sum of the squares of the other two sides (AC and BC).
This gives us the equation:
AB² = AC² + BC²
AB² = 5² + 5²
AB² = 25 + 25
AB² = 50
Taking the square root to solve for AB:
AB = √50 = √(25 * 2) = 5√2.
Calculating further, we find:
- 5√2 is approximately equal to 7.07 cm.
Correct Answer
However, since the options given in the problem do not include this calculated value, there is a misunderstanding in the interpretation of the problem or the options provided.
The correct answer, based on the problem description of an isosceles right triangle with the given side length, would indeed suggest that AB is longer than 5 cm but likely rounded or misinterpreted in the options.
Thus, while option B states 10 cm, it is essential to verify the context of the problem. The correct interpretation aligns closest with the calculated lengths, but option B is misleading.
Always double-check the context when dealing with geometric problems!
|
Explore Courses for SSC CGL exam
|
|
Top Courses for SSC CGLView all
Question Description
If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer? for SSC CGL 2025 is part of SSC CGL preparation. The Question and answers have been prepared according to the SSC CGL exam syllabus. Information about If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for SSC CGL 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer?.
If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer? for SSC CGL 2025 is part of SSC CGL preparation. The Question and answers have been prepared according to the SSC CGL exam syllabus. Information about If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for SSC CGL 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer?.
Solutions for If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC CGL.
Download more important topics, notes, lectures and mock test series for SSC CGL Exam by signing up for free.
Here you can find the meaning of If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is :a)5 cmb)10 cmc)52 cmd)2.5 cmCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice SSC CGL tests.
|
|
Explore Courses for SSC CGL exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup